Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
Khi ω = ω 1 thì điện áp hai đầu đoạn mạch AN và MB vuông pha nhau :
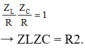
→
ta chuẩn hóa 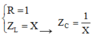
Kết hợp với
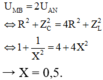
Khi ![]() (ta giả sử rằng
(ta giả sử rằng ![]() ) thì điện áp trên hai đầu cuộn cảm đạt cực đại
) thì điện áp trên hai đầu cuộn cảm đạt cực đại
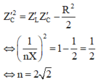
→ Vậy ω 1 = 50 π r a d / s .

Đáp án B
khi thay đổi C để U AP không phụ thuộc biến trở R. Dễ có Z C = 2 Z L
+ Khi R thay đổi ta luôn có tam giác APB luôn là tam giác cân tại A (Hình vẽ)

Ta thấy khi R thay đổi, nếu ta di chuyển điểm A→M thì góc 2φ chính là độ lệch pha của U AP và U AB càng lớn. Vậy độ lệch pha cực đại của U AP và U AB khi điểm A trùng với điểm M hay lúc đó R=0
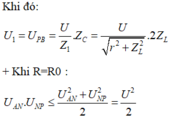
Vậy U AN . U NP lớn nhất khi U AN = U NP hay khi đó tam giác APB là tam giác vuông cân
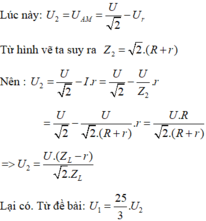
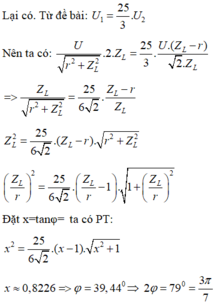

Chọn đáp án C
Khi ω = ω 1 thì điện áp hai đầu đoạn mạch AN và MB vuông pha nhau Z L R Z C R = 1 → Z L Z C = R 2
→ ta chuẩn hóa R = 1 Z L = X → Z C = 1 X
Kết hợp với U M B = 2 U A N ⇔ R 2 + Z C 2 = 4 R 2 + Z L 2 ⇔ 1 + 1 X 2 = 4 + 4 X 2
→ X = 0 , 5
Khi ω = ω 1 = 100 π 2 r a d / s (ta giả sử rằng ω 2 = n ω 1 ) thì điện áp trên hai đầu cuộn cảm đạt cực đại
Z ' C 2 = Z ' L Z ' C − R 2 2 ⇔ 1 n X 2 = 1 − 1 2 = 1 2 ⇔ n = 2 2
→ Vậy ω 1 = 50 π r a d / s

Đáp án A
+ Áp dụng kết quả bài toán chuẩn hóa ω biến thiên thể U R L max
→ U A N max có nghĩa là U R L max với n = 1 2 + 1 4 + 1 2 R 2 L C , kết hợp với
11 L = 50 C R 2 → n = 1 , 1
+Với n = f R L 2 f R 2 ⇒ f R = f R L 2 = 30 11 1 , 1 = 30 10 H z .
→ n - 1 2 2 = f R 2 f R C 2 - 1 2 2 = f R 2 f 1 2 - 1 2 2 f R 2 f 2 2 - 1 2 2 → f 1 = 100 H z .
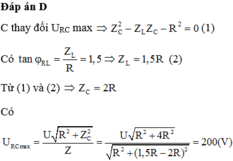
Chọn B
+ Áp dụng BHD ta có U RLmax ≈ 180 V.