Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Sử dụng định luật Ôm và các biến đổi toán học
Cách giải:
Khi thay đổi C để U AP không phụ thuộc biến trở R. Dễ có Z C = 2 Z L
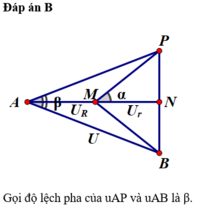
+ Khi R thay đổi ta luôn có ΔAPB luôn là tam giác cân tại A (Hình vẽ)
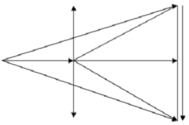
Ta thấy khi R thay đổi, nếu ta di chuyển điểm A→M thì góc 2φ chính là độ lệch pha của U AP và U AB càng lớn.
Vậy độ lệch pha cực đại của U AP và U AB khi điểm A trùng với điểm M hay lúc đó R = 0. Khi đó:
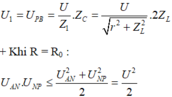
Vậy U AN . U NP lớn nhất khi U AN = U NP hay khi đó tam giác APB là tam giác vuông cân
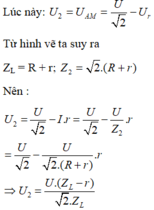
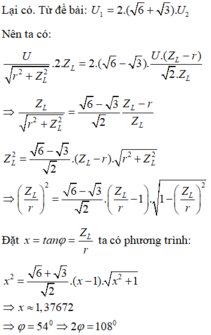

Đáp án B
+ Khi C = C 1 thì điện áp hiệu dụng hai đầu biến trở: U R = I . R = U . R R 2 + Z L − Z C 1 2 = U 1 + Z L − Z C 1 2 R 2
Để U R không phụ thuộc vào R thì: Z L − Z C 1 = 0 ⇒ Z C 1 = Z L 1
+ Khi C = C 2 thì điện áp hiệu dung hai đầu đoạn mạch chứa L và R:
U LR = I . R 2 + Z L 2 = U . R 2 + Z L 2 R 2 + Z L 2 − 2 Z L Z C 2 + Z C 2 2 = U 1 + − 2 Z L Z C 2 + Z C 2 2 R 2 + Z L 2
Để U R không phụ thuộc vào R thì: − 2 Z L Z C 2 + Z C 2 2 = 0 ⇒ Z C 2 = 2 Z L 2
Từ (1) và (2) ta có: Z C 1 Z C 2 = C 2 C 1 = 1 2 ⇒ 2 C 2 = C 1

Đáp án C
Sử dụng giản đồ vecto trong dòng điện xoay chiều
Khi C = C 1 thì điện áp trên hai đầu R không phụ thuộc R, chứng tỏ có cộng hưởng. U R = U AB → Z C 1 = Z L
Khi C = C 2 thì điện áp trên hai đầu R L không phụ thuộc R, chứng tỏ U LR = U AB
Ta có giản đồ vecto
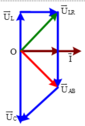
Từ giản đồ thấy được U C 2 = 2 U L
![]()

Đáp án A
Khi L = L 1 → U R = IR = UR R 2 + Z L 1 − Z C 2 = U 1 + Z L 1 − Z C 2 R 2
Để U R không phụ thuộc R thì Z L 1 − Z C = 0 → Z L 1 = Z C *
Khi L = L 2 → U R C = I R 2 + Z C 2 = U R 2 + Z C 2 R 2 + Z L 2 − Z C 2 = U 1 + Z L 2 2 − 2 Z L 2 Z C R 2 + Z C 2
Để U R C không phụ thuộc R thì Z L 2 = 2 Z c * *
Từ (*) và (**) → Z L 2 = 2 Z L 1 → L 2 = 2 L 1



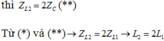

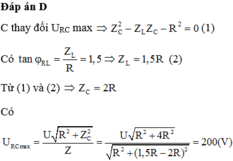
Đáp án B
khi thay đổi C để U AP không phụ thuộc biến trở R. Dễ có Z C = 2 Z L
+ Khi R thay đổi ta luôn có tam giác APB luôn là tam giác cân tại A (Hình vẽ)
Ta thấy khi R thay đổi, nếu ta di chuyển điểm A→M thì góc 2φ chính là độ lệch pha của U AP và U AB càng lớn. Vậy độ lệch pha cực đại của U AP và U AB khi điểm A trùng với điểm M hay lúc đó R=0
Vậy U AN . U NP lớn nhất khi U AN = U NP hay khi đó tam giác APB là tam giác vuông cân