
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

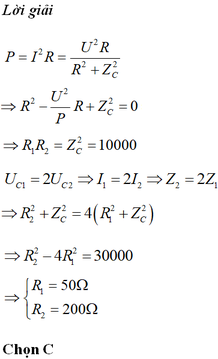

R 1 R 2 = 100 2 U C 1 = 2 U C 2 ⇒ R 1 R 2 = 100 2 I 1 = 2 I 2 ⇒ R 1 R 2 = 100 2 R 2 2 + 100 2 = 4 R 1 2 + 4.100 2
→ Ta có phương trình R 2 2 − 2 R 1 R 2 − 4 R 1 2 = 0
→ R 2 = 4 R 1 .
Thay vào phương trình trên, ta tìm được R 1 = 50 Ω v à R 2 = 200 Ω .
Đáp án C

- Hai giá trị của R cho cùng công suất tiêu thụ trên mạch thỏa mãn

- Kết hợp với:
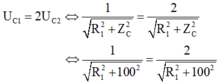
- Từ hai phương trình trên, ta thu được:
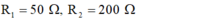

Đáp án B
+ Hai giá trị của R cho cùng công suất tiêu thụ trên mạch thỏa mãn ![]()
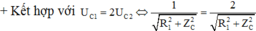
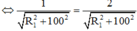
Từ hai phương trình trên, ta thu được ![]()

Ta áp dụng kết quả sau:
Mạch RLC có R thay đổi, khi R = R1 hoặc R = R2 thì công suất của mạch như nhau là P, khi đó:
\(\begin{cases}R_1+R_2=\frac{U^2}{P}\\R_1R_2=\left(Z_L-Z_C\right)^2\end{cases}\)
\(\Rightarrow R_1R_2=Z_C^2=100^2\)(1)
Điện áp hiệu dụng giữa hai đầu tụ điện: \(U_C=IZ_C=\frac{U.Z_C}{\sqrt{R^2+Z_C^2}}\)
\(U_{C1}=2U_{C2}\)
\(\Rightarrow\frac{U.Z_C}{\sqrt{R_1^2+Z_C^2}}=\frac{2U.Z_C}{\sqrt{R^2_2+Z_C^2}}\)
\(\Rightarrow2\sqrt{R_1^2+Z_C^2}=\sqrt{R_2^2+Z_C^2}\)
\(\Rightarrow4\left(R_1^2+100^2\right)=\left(R_2^2+100^2\right)\)
\(\Rightarrow4R_1^2-R_2^2=-3.100^2\)
Rút R2 ở (1) thế vào pt trên ta đc:
\(4R_1^2-\frac{100^4}{R_1^2}=-3.100^2\)
\(\Rightarrow4R_1^4+3.100^2.R_1^2-100^4=0\)
\(\Rightarrow R_1=50\Omega\)
\(\Rightarrow R_2=20\Omega\)

Đáp án A
Dựa vào đồ thị, ta thấy khi 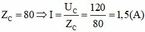
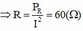
Mặt khác, khi Z C tiến đến vô cùng, U C tiệm cận đến 120V. Có

nên khi Z C tiến đến vô cùng, U C = U => U = 120 (V).
Suy ra khi
Z
C
= 80 thì ta có : ![]()
![]()
![]()
![]()
C thay đổi, U C max
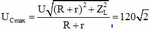

Đáp án D
+ Ta có: ![]()
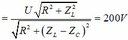
+ Từ đồ thị ta thấy
U
R
L
không phụ thuộc R: 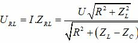
+ Khi ![]()
![]()
![]()

Ta có n = R 2 R 1 = 4 → P = n n + 1 2 P max ⇒ P m a x = 125 W
Đáp án A