Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
. Khi tần số f = f3 = 180 Hz thì hệ số công suất của mạch gần với giá trị nào sau đây nhất ?
Đáp án D
Ta chuẩn hóa số liệu:
+ f =
f
1
= 60 Hz: Đặt R = 1 thì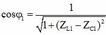 
+ f =
f
2
= 120 Hz: có 
+ f =
f
3
= 180 Hz: có
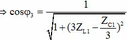
Theo đề bài: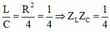 
Có 
Từ (1) và (2) tìm được 
Thay vào cos
φ
3
= 0,923
Dựa vào giản đồ xét tam giác vuông OAB có
\(\sin60=\frac{Uc}{U_{ }AB}\Rightarrow U_C=100.\sin60=50\sqrt{3}V\Rightarrow Z_C=\frac{U_C}{I}=\frac{50\sqrt{3}}{0.5}=100\sqrt{3}\Omega\)
=> \(C=\frac{1}{Z_C.\omega}\)
\(\cos60=\frac{U_R}{U_{AB}}\Rightarrow U_R=50\Omega\Rightarrow R=\frac{U_R}{I}=100\Omega\)
2. Công suất trên mạch có biểu thức
\(P=I^2R=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R\\=\frac{U^2}{R^{ }+\frac{\left(Z_L-Z_C\right)^2}{R}}\)
L thay đổi để P max <=> Mẫu Min => áp dụng bất đẳng thức cô-si cho hai số không âm=> \(R=\left|Z_L-Z_C\right|\)
=> \(R=100-40=60\Omega\)
=>
Em phải post mỗi câu hỏi 1 bài thôi nhé, để tiện thảo luận.
1. Điều kiện có sóng dừng trên dây có một đầu cố định một đầu tự do: \(L=(2n+1)\frac{\lambda}{4}=(2n+1)\frac{v}{4f}\) (L là chiều dài dây)
\(\Rightarrow n=\frac{1}{2}(\frac{4fL}{v}-1)\)
Do f từ 80Hz đến 120 Hz nên ta tìm được n thỏa mãn sẽ từ 12 đến 17
Do đó có 6 tần số có thể tạo sóng dừng trên dây.
2. Điều chỉnh C để công suất cực đại --> Cộng hưởng xảy ra ---> \(P=\dfrac{U^2}{R}=600(W)\)
Điều chỉnh C = C2 thì công suất sẽ là: \(P_2=\dfrac{U^2}{R}\cos^2(\varphi)=600.(\dfrac{\sqrt 3}{2})^2=450W\)
Ta có: cos φ = 2 m − 1 m = 1 3 ⇒ m ≈ 0 , 55
→ Với m = f C f L = f 0 f 0 + 5 6 = 0 , 55 → S H I F T + S O L V E f 0 = 15 Hz
Đáp án B
Đáp án A
f
L
thì
U
L
max;
f
L
1
và
f
L
2
thì
U
L
như nhau thì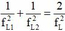 
Tương tự với
U
C
, có 
Để ý thấy, f thay đổi làm cho U L = U thì f L 1 = ∞; U C = U thì f C 1 = 0
Suy ra 
Với các bài toán xảy ra công thức (1), ta đều có Z L , Z C đổi chỗ cho nhau trong 2 trường hợp tần số f L , f C . Đồng thời cosφ trong cả 2 trường hợp cũng bằng nhau.
Đặt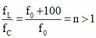 
Có 
Có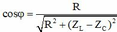 
Mặt khác 
Từ 2 pt trên, dễ dàng tìm được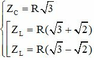 
Vì n > 1 nên Z L > Z C => chọn
Từ đó tính được 
Khi tăng điện dung nên 2.5 lần thì dung kháng giảm 2.5 lần. Cường độ dòng trễ pha hơn hiệu điện thế $\pi/4$ nên
$Z_L-\frac{Z_C}{2.5}=R$
Trường hợp đầu tiên thì thay đổi C để hiệu điện thế trên C cực đại thì $Z_LZ_C=R^2+Z_L^2$
$Z_LZ_C=(Z_L-\frac{Z_C}{2.5})^2+Z_L^2$
Giải phương trình bậc 2 ta được: $Z_C=\frac{5}{4}Z_L$ hoặc $Z_C=10Z_L$(loại vì Zl-Zc/2.5=R<0)
$R=\frac{Z_L}{2}$
Vẽ giản đồ vecto ta được $U$ vuông góc với $U_{RL}$ còn $U_C$ ứng với cạch huyền
Góc hợp bởi U và I bằng với góc hợp bởi $U_L$ và $U_{LR}$
$\tan\alpha=\frac{R}{Z_L}=0.5$
$\sin\alpha=1/\sqrt5$
$U=U_C\sin\alpha=100V$
\(U_{C}{max}=\frac{U\sqrt{R^{2}+Z_L^{2}}}{R}\); \(Zc=\frac{R^{2}+Z_L^{2}}{Z_L}\)
khi C2=2,5C1---->Zc2=Zc1/2,5=ZC/2,5
do i trể pha hơn U nên Zl>Zc/2,5
\(\tan\frac{\pi }{4}=\frac{Z_L-0,4Zc}{R}=1\Rightarrow R=Z_L-0,4Z_C\)
\(\Rightarrow Z_C.Z_L=Z_L^{2}+(Z_L-0,4Z_C)^{2}\Rightarrow 2Z_L^{2}-1,8Z_CZ_L+0,16Z_C^{2}=0\Rightarrow Z_L=0,8Z_C;Z_L=0,1Z_C\)(loai)
\(\Rightarrow R=Z_L-1,25.0,4Z_L=0,5Z_L\)
\(\Rightarrow U_{C}{max}=\frac{U\sqrt{Z_L^{2}+0,25Z_L^{2}}}{0,5Z_L}=100\sqrt{5}\Rightarrow U=100V\)
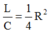
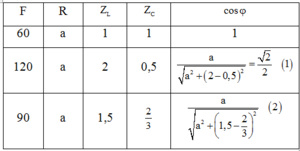
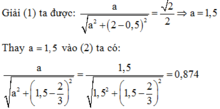
Đáp án D
Chuẩn hóa R = 1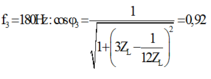
Ta có