Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt đề : Vẽ tam giác đều ABC . Vẽ tam giác ABD vuông cân tại B(D và C nằm khác phía đối với AB)
Vẽ tam giác ACE vuông cân tại C ( E và B nằm khác phía đối với AC )
Đo góc DAE = 150o

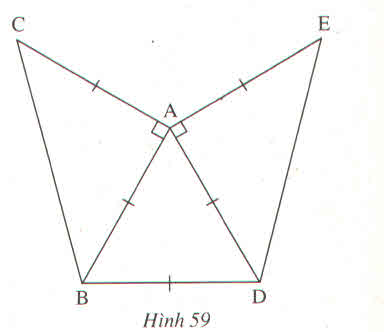
Đề: Cho tam giác đều ABC. Vẽ DB vuông góc với AB tại B, EC vuông góc với AC tại C sao cho AB = DB, AC = EC. Tính số đo góc DAE.
Giải:
GT: \(\Delta ABC\) đều
\(AB\perp DB\)
\(AC\perp CE\)
AB = DB
AC = EC
KL: \(\widehat{DAE}=?\)
Ta có:
\(\Delta ABC\) đều => \(\widehat{A_2}=\widehat{B_2}=\widehat{C_2}=60^o\)
\(\Delta ABD\) có \(\widehat{B_1}=90^o\), AB = DB => \(\Delta ABD\) vuông cân tại B
=> \(\widehat{A_1}=45^o\)
\(\Delta ABD\) có \(\widehat{C_1}=90^o\), AB = DB => \(\Delta ABD\) vuông cân tại B
=> \(\widehat{A_1}=45^o\)
\(\Delta ACE\) có \(\widehat{C_1}=90^o\), AC = EC => \(\Delta ACE\) vuông cân tại C
=> \(\widehat{A_3}=45^o\)
=> \(\widehat{DAE}=\widehat{A_1}+\widehat{A_2}+\widehat{A_3}=45^o+60^o+45^o=150^o\)

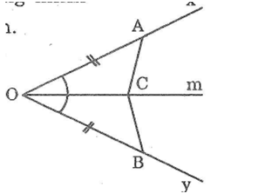
Cho góc nhọn xOy. Trên tia Ox lấy điểm A trên tia Oy lấy điểm B sao cho OA = OB. Lấy điểm C bất kì trên tia phân giác Om của góc xOy. Chứng minh rằng ΔAOC = ΔBOC

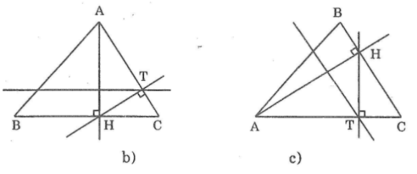
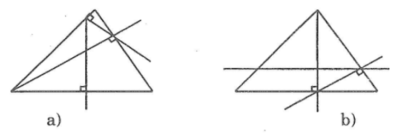
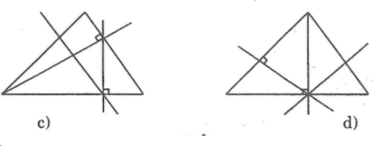
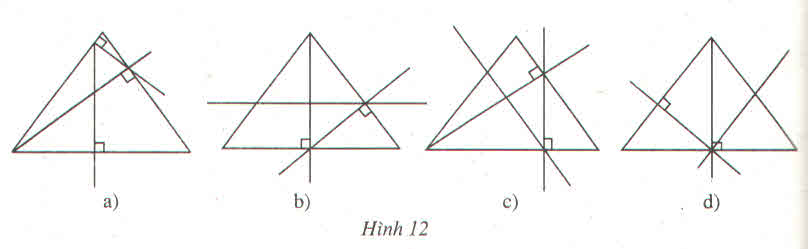
Hình a sai ; Hình b đúng ; Hình c đúng ; Hình d sai
Tên các điểm được thể hiện trong hình dưới:

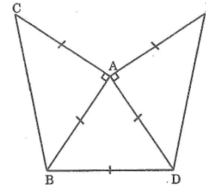
- Vẽ tam giác ABC vuông cân tại A
- Vẽ tam giác đều ABD sao cho D và C nằm trên 2 nửa mặt phẳng có bờ chứa đường thẳng AB.
- Vẽ tam giác vuông cân ADE sao cho E và B nằm trên 2 nửa mặt phẳng đối bờ chứa đường thẳng AD.
Chứng minh tam giác ACE là tam giác cân.

- Ta có: \(\widehat{xOz}=180^o-\widehat{zOb}\) (Hai góc kề bù)
\(\widehat{zOb}=180^o-\widehat{xOz}\)
- Vì Oy là tia phân giác của góc xOz
\(\Rightarrow\widehat{xOy}=\widehat{yOz}=\frac{\widehat{xOz}}{2}=\frac{180^o-\widehat{zOb}}{2}=90^o-\frac{1}{2}\widehat{zOb}\) (1)
- Vì Oa là tia phân giác của góc zOb
\(\Rightarrow\widehat{zOa}=\widehat{aOb}=\frac{\widehat{zOb}}{2}=\frac{180^o-\widehat{xOz}}{2}=90^o-\frac{1}{2}\widehat{xOz}\) (2)
- Từ (1) và (2), suy ra:
\(\widehat{yOz}+\widehat{zOa}=90^o-\frac{1}{2}\widehat{zOb}+90^o-\frac{1}{2}\widehat{xOz}\)
\(\Rightarrow\widehat{yOa}=180^o-\frac{1}{2}\left(\widehat{zOb}+\widehat{xOz}\right)\)
\(\Rightarrow\widehat{yOa}=180^o-\frac{1}{2}\left(180^o\right)\)
\(\Rightarrow\widehat{yOa}=180^o-90^o\)
\(\Rightarrow\widehat{yOa}=90^o\)
\(\Rightarrow Oy\perp Oa\Rightarrowđpcm\)



Đề toán:
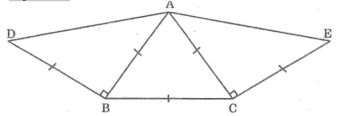
Vẽ tam giác ABC đều
Vẽ tam giác ABD vuông cân tại B sao cho D và C nằm trên hai nửa mặt phẳng bờ chứa đường thẳng AB.
Vẽ tam giác ACE vuông cân tại C sao cho E và B nằm trên hai nửa mặt phẳng đối có bờ chứa đường thẳng AC
Đo ∠DAE =150o
Chứng minh: