Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Tại thời điểm t 1 thì:
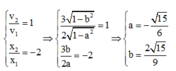
Dễ thấy a và b trái dấu, để đơn giản chọn a < 0 => b > 0
Ta có:
![]()
Tại thời điểm t 2
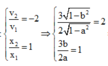
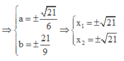

Giải thích: Đáp án D
Phương pháp: Sử dụng hê ̣thức độc lập theo thời gian của x và v
Cách giải:
- Tại thời điểm t:
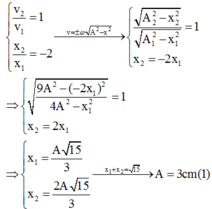
- Tại thời điểm t + ∆t: 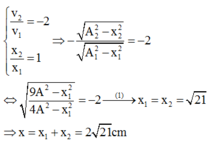

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Áp dụng công thức (5.1 và 5.2 - SGK) ta tìm được:
A = 2,3 cm và φ = 0,73π
Phương trình dao động tổng hợp là: x = 2,3cos(5πt + 0,73π) (cm).

Áp dụng công thức độc lập, ta có: \(A^2 = x^2+\frac{v^2}{\omega^2} \Rightarrow\) \(8^2+\frac{12^2}{\omega^2} = 6^2+\frac{16^2}{\omega^2} \Rightarrow \omega = 2 \ (rad/s) \Rightarrow f = \frac{1}{\pi} \ Hz\)

 chọn A
chọn A
Đáp án A
Đặt a = cos(ωt + φ1) và b = cos(ωt + φ2)
Tại thời điểm t1 thì:
Dễ thấy a và b trái dấu,
để đơn giản chọn a < 0 => b > 0.
Ta có: x = x1 + x2 = A(2a + 3b)
= -2Aa = 15 => A = 3 cm
Tại thời điểm t2 thì: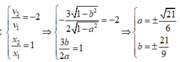
Nhận thấy trường hợp này a, b cùng dấu. Dựa vào 4 đáp án => lấy a > 0, b > 0.
Vậy khi đó ta có li độ dao động tổng hợp: