Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích: Đáp án D
Phương pháp: Sử dụng hê ̣thức độc lập theo thời gian của x và v
Cách giải:
- Tại thời điểm t:
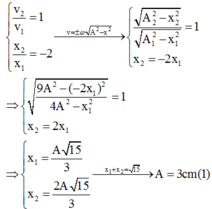
- Tại thời điểm t + ∆t: 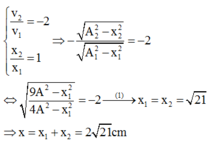

Đáp án A
Đặt a = cos(ωt + φ1) và b = cos(ωt + φ2)
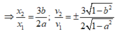
Tại thời điểm t1 thì:
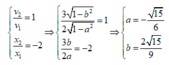
Dễ thấy a và b trái dấu,
để đơn giản chọn a < 0 => b > 0.
Ta có: x = x1 + x2 = A(2a + 3b)
= -2Aa = 15 => A = 3 cm
Tại thời điểm t2 thì: 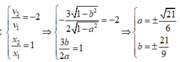
Nhận thấy trường hợp này a, b cùng dấu. Dựa vào 4 đáp án => lấy a > 0, b > 0.
Vậy khi đó ta có li độ dao động tổng hợp:
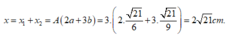

Chọn đáp án D
Tại t: dao động thứ hai có vận tốc là:
− 20 π 3 c m / s = − V 2 max 2 . 3 cm/s
và tốc độ đang giảm nên tại t pha dao động thứ 2 là 2π/3 rad.
Mà x1 và x2 lệch pha nhau π/3 suy ra tại t thì pha của x1 là π/3.
Suy ra A 1 = 3.2 = 6 cm.
A = A 1 2 + A 2 2 + 2 A 1 A 2 cos φ = 6 2 + 10 2 + 2.6.10. cos π 3 = 14 c m
Suy ra khi pha dao động tổng hợp là − 2 π 3 thì li độ dao động tổng hợp là:
x = A . cos − 2 π 3 = − 7 c m .

Chọn C
+ Tổng hợp dao động x = x1 + x2 => x2 = x – x1 = (-3) – 2 = - 5cm.
=> dao động tổng hợp luôn cùng pha với dao động thứ hai. Li độ dao động thứ hai khi x = 4,5cm là: x2 = 4,5.-5/-3 = 7,5cm.

Đáp án D
Phương pháp: Sử dụng̣ giản đồ Fresnen
Cách giải:
x1 + x2 = x => x1 +6 = 9cm => x1 = 3cm
Dựa vào đề bài ta biểu diễn được các vecto dao động như hình bên:
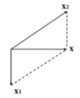
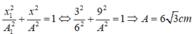

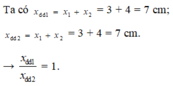
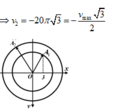
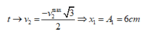
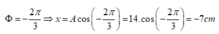
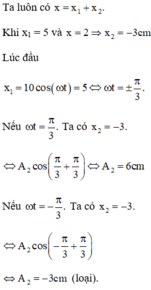
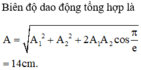
Đáp án D
Tại thời điểm t 1 thì:
Dễ thấy a và b trái dấu, để đơn giản chọn a < 0 => b > 0
Ta có:
Tại thời điểm t 2