Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi v1 = 2 m/s = 7.2 km/h
Thời gian đi 4km đầu là \(\dfrac{4}{7,2}\) = \(\dfrac{5}{9}\)(h)
Vận tốc trung bình của người đó là \(\dfrac{s_1 + s_2}{t_1 + t_2} = \dfrac{4 + 2}{\dfrac{5}{9} + \dfrac{1}{3}} = 6.75 (km/h)\)
đổi 2m/s=7,2km/h=> thời gian đi hết quãng đường đầu tiên :\(\dfrac{4}{7,2}=\dfrac{5}{9}\)(giờ)
=> Vận tốc trung bình người đó
Vtb=\(\dfrac{4+2}{\dfrac{5}{9}+\dfrac{1}{3}}=\dfrac{6}{\dfrac{8}{9}}=\dfrac{6.9}{8}=6,75km\)/giờ

Ta chia quãng đường từ A đến B làm sáu phần mỗi phần gọi là: \(s\left(km\right)\)
Cả quãng đường AB là: \(6s\left(km\right)\)
Gọi t là thời gian người đó đi trong \(\dfrac{1}{3}\) quãng đường
Thời gian người đó đi trên quãng đường AB là: \(3t\left(h\right)\)
Trong \(\dfrac{1}{3}\) thời gian người đó đi với vận tốc v2 :
\(s_2=\dfrac{1}{3}\cdot6s=2s\left(km\right)\)
Quãng đường mà người đó đi với vận tốc v3 :
\(s_3=\dfrac{1}{2}\cdot6s=3s\left(km\right)\)
Mà: \(s_1+s_2+s_3=s_{AB}\)
Quãng đường mà người đó đi được với vận tốc 20km/h:
\(s_1=s_{AB}-s_2-s_3=6s-2s-3s=s\left(km\right)\)
Giá trị của 1 trong 6 phần quãng đường AB là:
\(s=20\cdot\dfrac{1}{3}\cdot3t=20t\left(km\right)\)
Ta có tổng quãng đường đi là:
\(s_1+s_2+s_3=6s\left(km\right)\)
Tổng thời gian mà người đó đi là:
\(t_1+t_2+t_3=3t\left(h\right)\)
Vận tốc trung bình của người đó trên cả quãng đường:
\(v_{tb}=\dfrac{s_{AB}}{t}=\dfrac{6s}{3t}=\dfrac{2s}{t}\left(km/h\right)\)
Mà: \(s=20t\left(km\right)\) thay vào ta có:
\(v_{tb}=\dfrac{2\cdot20t}{t}=2\cdot20=40\left(km/h\right)\)
Vận tốc v2 không thể nhỏ hơn giá trị của v1 là 20 km/h.

Gọi s là chiều dài nửa quãng đường mà người đi xe đạp phải đi.
Như vậy, thời gian đi hết nửa quãng đường đầu s1 = s với vận tốc v1 là:

Thời gian đi hết nửa quãng đường còn lại s2 = s với vận tốc v2 là:

Vậy tổng thời gian đi hết cả quãng đường là: 
Vận tốc trung bình của người đi xe đạp trên cả quãng đường là:

Giải
Gọi s là chiều dài nửa quãng đường
Thời gian đi hết nửa quãng đường đầu với vận tốc v1 là t1=s/v1 (1)
Thời gian đi hết nửa quãng đường còn lại với vận tốc v2 là t2=s/v2 (2)
Vận tốc trung bình của người đi xe đạp trên quãng đường là vtb = 2s/t1+ t2 (3)
Kết hợp (1); (2); (3) có: 1/v1 + 1/v2 = 2/vtb
Thay số vtb = 8km/h ; v1 = 12km/h
Vận tốc trung bình của người đi xe ở nửa quãng đường sau là v2 = 6km/h.

Gọi vận tốc dự định cần tìm là x(km/h) \(\left(x>10\right)\)
Thời gian đi dự định: \(\dfrac{60}{x}\left(h\right)\)
+Quãng đường xấu dài: \(60\cdot\dfrac{1}{3}=20km\)
Khi đó vận tốc bị giảm đi 10km/h\(\Rightarrow v'=x-10\) (km/h)
\(\Rightarrow\)Thời gian đi đoạn đường xấu: \(t'=\dfrac{20}{x-10}\left(h\right)\)
+Quãng đường còn lại: \(60-20=40km\)
Thời gian đi: \(t=\dfrac{40}{x}\left(h\right)\)
Do đó hai bố con về quê chậm hơn 10 phút \(=\dfrac{1}{6}h\):
\(\Rightarrow\left(\dfrac{40}{x}+\dfrac{20}{x-10}\right)-\dfrac{60}{x}=\dfrac{1}{6}\)
\(\Rightarrow\dfrac{20}{x-10}-\dfrac{20}{x}=\dfrac{1}{6}\Rightarrow x^2-10x-1200=0\)
\(\Rightarrow\left[{}\begin{matrix}x=40\left(tm\right)\\x=-30\left(loại\right)\end{matrix}\right.\)
Vậy vận tốc dự định của hai bố con là 40km/h.
bạn copy sao không ghi tham khảo zậy
copy nên chỗ nào gõ latex nó sẽ lặp 2 lần nha, lần sau bạn chú ý

Đổi 4,8km = 4800m
Thời gian đến trường :
Ta có: \(v=\dfrac{s}{t}\Leftrightarrow t=\dfrac{s}{v}=\dfrac{4800}{2}=2400\left(s\right)=\dfrac{2}{3}\left(h\right)\)
⇒ Chọn C
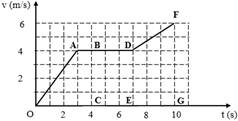
Vận tốc trung bình trên đoạn đường thứ nhất là :
\(V_{tb_1}=\dfrac{S_1}{t_1}=\dfrac{200}{60+40}=2m/s\)
Vận tốc trung bình trên đoạn đường thứ hai là :
\(V_{tb_2}=\dfrac{S_2}{t_2}=\dfrac{300}{100}=3m/s\)
Vận tốc trung bình trên cả đoạn đường là:
Vận tốc trung bình trên cả đoạn đường là :
\(V_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{200+300}{100+100}=2,5m/s\)