Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(A=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}=1+\dfrac{4}{\sqrt{x}-2}\)
Để A nguyên thì 4 ⋮ √x - 2
\(\Rightarrow\sqrt{x}-2\inƯ\left(4\right)\)
\(\Rightarrow\sqrt{x}-2\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{3;1;4;0;6;-2\right\}\)
Mà x \(\sqrt{x}\ge0\)
=> x thuộc {9; 1; 16; 0; 36}
b)

a) \(P\)\(=\sqrt{x}-2+3-3\sqrt{x}=1-2\sqrt{x}\)
b) \(Q=\frac{2\left(1-2\sqrt{x}\right)}{1-1+2\sqrt{x}}=\frac{1-2\sqrt{x}}{\sqrt{x}}=\frac{1}{\sqrt{x}}-2\)
vậy x=1 thỏa mãn đề bài.
Trả lời :.............................
x=1...........................
Hk tốt..............................

a ) \(ĐKXĐ:x\ge0;x\ne1\)
= \(\frac{x+1+\sqrt{x}}{x+1}:\left[\frac{1}{\sqrt{x}-1}-\frac{2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}\right]-1\)
\(=\frac{x+1+\sqrt{x}}{x+1}:\frac{x+1-2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}-1\)
\(=\frac{x+1+\sqrt{x}}{x+1}:\frac{\left(\sqrt{x}-1\right)^2}{\left(x+1\right)\left(\sqrt{x}-1\right)}-1\)
\(=\frac{\left(x+1+\sqrt{x}\right)\left(x+1\right)\left(\sqrt{x}-1\right)}{\left(x+1\right)\left(\sqrt{x}-1\right)^2}-1\)
\(=\frac{x+1+\sqrt{x}}{\sqrt{x}-1}-1=\frac{x+2}{\sqrt{x}-1}\)
B ) Ta có :
\(Q=P-\sqrt{x}\)
\(=\frac{\sqrt{x}+2}{\sqrt{x}-1}-\sqrt{x}\)
\(=\frac{\sqrt{x}+2}{\sqrt{x}-1}=\frac{\left(\sqrt{x}-1\right)+3}{\sqrt{x}-1}=1+\frac{3}{\sqrt{x}-1}\)
Đế Q nhận giá trị nguyên thì \(1+\frac{3}{\sqrt{x}-1}\in Z\)
\(\Leftrightarrow\frac{3}{\sqrt{x}-1}\in Z\left(vì1\in Z\right)\)
\(\Leftrightarrow\sqrt{x}-1\inƯ\left(3\right)\)
Ta có bảng sau :
| \(\sqrt{x}-1\) | 3 | -3 | 1 | -1 |
| \(\sqrt{x}\) | 4 | -2 | 2 | 0 |
| \(x\) | 16(t/m) | 4(t/m) | 0(t/m) |
Vậy để biểu thức \(Q=P-\sqrt{x}\) nhận giá trị nguyên thì \(x\in\left\{16;4;0\right\}\)

Chỉ làm thử thôi nhé-.-
\(B=\left(\sqrt{x+2-4\sqrt{x-2}}+\sqrt{x+2+4\sqrt{x-2}}\right):\sqrt{\frac{4}{x^2}-\frac{4}{x}+1}\left(đk:x\ge2\right)\)
\(=\left(\sqrt{x-2-2\sqrt{x-2}.2+2^2}+\sqrt{x-2+2\sqrt{x-2}.2+2^2}\right):\sqrt{\frac{4}{x^2}-\frac{4x}{x^2}+\frac{x^2}{x^2}}\)
\(=[\left(\sqrt{\left(\sqrt{x-2}-2\right)^2}+\sqrt{\left(\sqrt{x-2}+2\right)^2}\right):\sqrt{\frac{4-4x+x^2}{x^2}}\)
\(=\left(|\sqrt{x-2}-2|+|\sqrt{x-2}+2|\right):\sqrt{\frac{\left(2-x\right)^2}{x^2}}\)
\(=\left(\sqrt{x-2}-2+\sqrt{x-2}+2\right).\frac{x}{2-x}\)
\(=2\sqrt{x-2}.\frac{x}{2-x}=\frac{2x\sqrt{x-2}}{2-x}\)

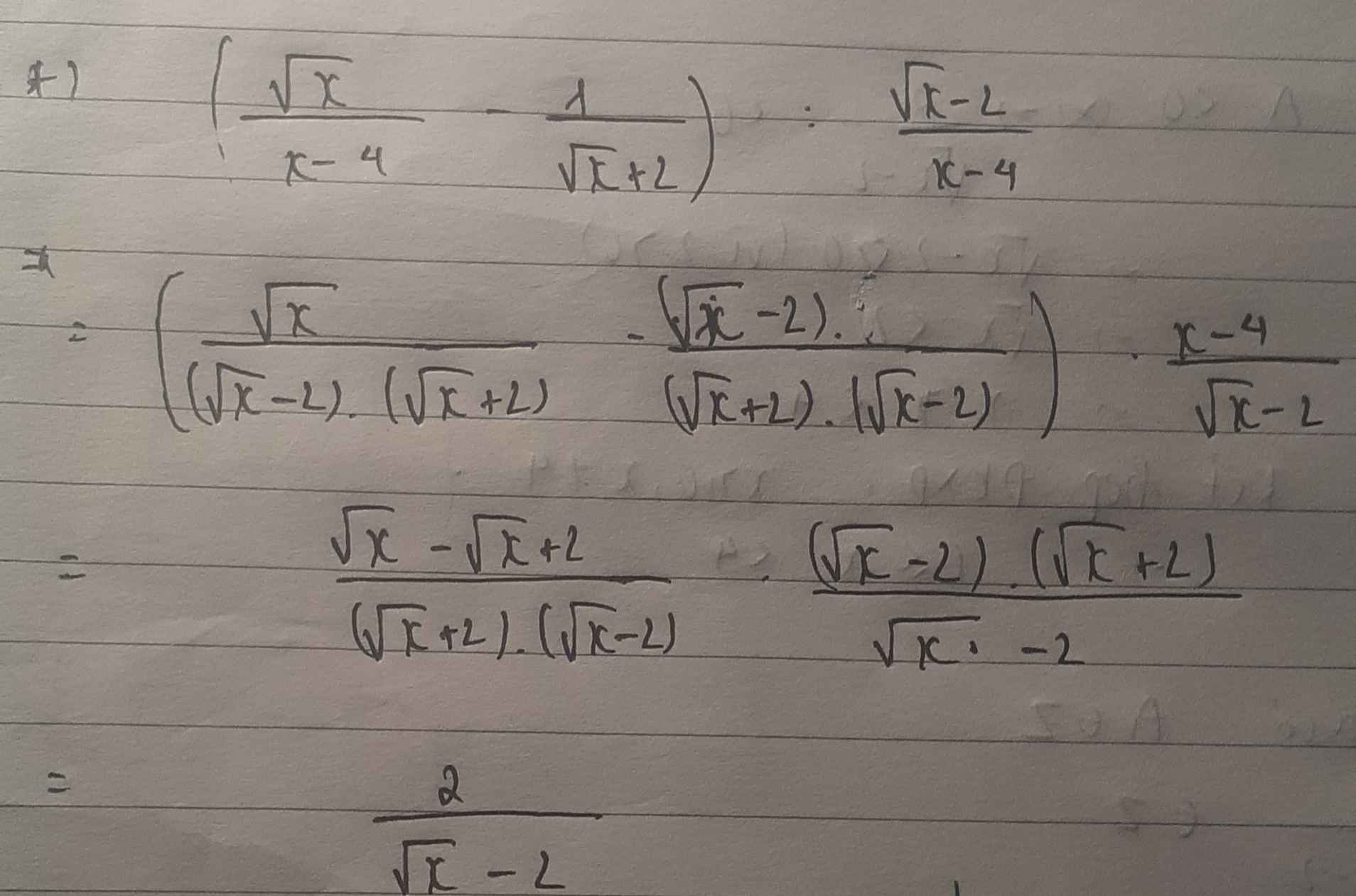

a) \(B=\left(\frac{\sqrt{x}}{x-4}+\frac{1}{\sqrt{x}-2}\right)\div\frac{\sqrt{x}+2}{x-4}\)
\(=\frac{\sqrt{x}+\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\frac{x-4}{\sqrt{x}+2}\)
\(=\frac{2\sqrt{x}+2}{x-4}\cdot\frac{x-4}{\sqrt{x}+2}=\frac{2\sqrt{x}+2}{\sqrt{x}+2}\)
b) \(C=A\left(B-2\right)=\frac{\sqrt{x}+2}{\sqrt{x}-2}\cdot\left(\frac{2\sqrt{x}+2}{\sqrt{x}+2}-2\right)\)
\(=\frac{\sqrt{x}+2}{\sqrt{x}-2}\cdot\frac{-2}{\sqrt{x}+2}=\frac{2}{2-\sqrt{x}}\)
Để C nguyên => \(2-\sqrt{x}\inƯ\left(2\right)\Rightarrow2-\sqrt{x}\in\left\{\pm1;\pm2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;1;3;4\right\}\Leftrightarrow x\in\left\{0;1;9;16\right\}\)