
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. f(\(\dfrac{-1}{2}\)) = \(4.\left(\dfrac{-1}{2}\right)^2+3.\left(\dfrac{-1}{2}\right)-2\)
= \(4.\dfrac{1}{4}-\left(\dfrac{-3}{2}\right)-\dfrac{4}{2}\)
= \(\dfrac{2}{2}+\dfrac{3}{2}-\dfrac{4}{2}\)
= \(\dfrac{1}{2}\)

Câu 1: A
Câu 2: D
Câu 3: C
Câu 4: A
Câu 5: A
Câu 6: B
Câu 7: C
Câu 8: D


`a) `
`P`(`x`)`=3x^3 -5x^2 -x^3 -6x+2`
`=2x^3 -5x^2 -6x+2`
`Q`(`x`)`=-2x^3 -7x +1 +2x^2 -x`
`=-2x^3 +2x^2 -8x+1`
`b)`
P(x) `+ `Q(x)`=(2x^3 -5x^2 -6x+2)+(-2x^3 +2x^2 -8x+1)`
`=2x^3 -5x^2 -6x+2-2x^3 +2x^2 -8x+1`
`=-3x^2 -14x+3`
P(x) `- `Q(x)`=(2x^3 -5x^2 -6x+2)-(-2x^3 +2x^2 -8x+1)`
`=2x^3 -5x^2 -6x+2+2x^3 -2x^2 +8x-1`
`=4x^3 -7x^2 +2x +1`

Vì Tam giác `DEF =` Tam giác `HIK ->`
\(\widehat{D}=\widehat{H}=73^0\)`, DE = HI = 5 cm, EF = IK = 7 cm`
Vậy, số đo \(\widehat{H}=73^0\)`,` độ dài `2` cạnh `HI` và `EF` lần lượt là `5 cm, 7 cm`
`\color{blue}\text {#DuyNam}`

\(\left|2x-3\right|=5-x\left(5-x\le0\right)\) ) ( * )
\(\left|2x-3\right|\le0\)
Mà \(\left|2x-3\right|\ge0\) với mọi \(x\) ( ** )
Từ ( * ) , ( ** ) dấu = phải xảy ra, khi đó ta có :
\(\left|2x-3\right|=0\)
\(2x-3=0\)
\(2x=3\)
\(x=\frac{3}{2}\)
Vậy \(x=\frac{3}{2}\)
Mình không chắc lắm !
| 2x - 3 | = 5 - x (*)
Xét hai trường hợp :
+) x < 3/2
(*) <=> -( 2x - 3 ) = 5 - x
<=> 3 - 2x = 5 - x
<=> -2x + x = 5 - 3
<=> -x = 2
<=> x = 2 ( thỏa mãn ) (1)
+) x ≥ 3/2
(*) <=> 2x - 3 = 5 - x
<=> 2x + x = 5 + 3
<=> 3x = 8
<=> x = 8/3 ( thỏa mãn ) (2)
Xét 5 - x ≤ 0
Ta có 5 - x ≤ 0 <=> -x ≤ -5 <=> x ≥ 5 (1)
So sánh (1), (2) với (3) ta thấy không có giá trị nào thỏa mãn
Vậy không có giá trị x thỏa mãn | 2x - 3 | = 5 - x và 5 - x ≤ 0

Bài 2:
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là tia phân giác của góc BAC
b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔANH
Suy ra: AM=AN
hay ΔAMN cân tại A
c: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
d: \(AH^2-AN^2=HN^2\)
\(BH^2-BM^2=MH^2\)
mà HN=MH
nên \(AH^2-AN^2=BH^2-BM^2\)
hay \(AH^2+BM^2=BH^2+AN^2\)
 dag cần gấp ạ! e c.ơn
dag cần gấp ạ! e c.ơn



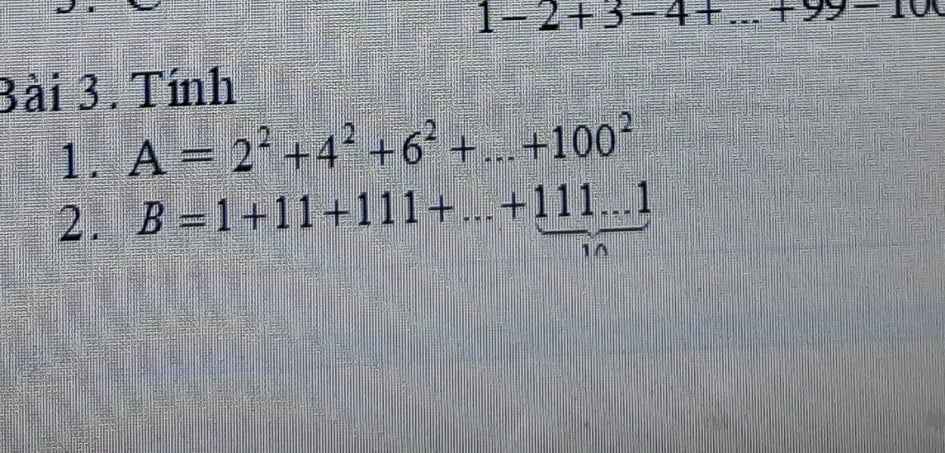 giúp em câu a. E tsu dag cần gấp mng giúp em với. Em cảm ơn
giúp em câu a. E tsu dag cần gấp mng giúp em với. Em cảm ơn

a, Vì AC⊥AB và BD⊥AB nên AC//BD
b, Vì AC//BD nên \(\widehat{D_1}=\widehat{ACD}\) (so le trong)
Mà \(\widehat{ACD}+\widehat{C_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{ACD}=\widehat{D_1}=180^0-70^0=110^0\)