HG
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LK
1
3 tháng 7 2019
Vì
\(\frac{1}{2}< \frac{2}{3};\frac{3}{4}< \frac{4}{5};\frac{5}{6}< \frac{6}{7};...;\frac{99}{100}< \frac{100}{101}\)
\(\Rightarrow\frac{1}{2}.\frac{3}{4}.\frac{5}{6}...\frac{99}{100}< \frac{2}{3}.\frac{4}{5}.\frac{6}{7}...\frac{100}{101}\)
\(\Rightarrow a< b\)
VD
20 tháng 3 2022
d, `3,15+2,4=5,55`
e, \(\dfrac{5}{7}.\dfrac{2}{11}+\dfrac{5}{7}.\dfrac{9}{11}=\dfrac{5}{7}\left(\dfrac{2}{11}+\dfrac{9}{11}\right)=\dfrac{5}{7}.\dfrac{11}{11}=\dfrac{5}{7}.1=\dfrac{5}{7}\)
f, `1,25.3,6+3,6.8,75=3,6(1,25+8,75)=3,6.10=36`
\(h,\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{99.100}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ =1-\dfrac{1}{100}\\ =\dfrac{99}{100}\)
20 tháng 3 2022
\(e\dfrac{5}{7}\times\left(\dfrac{2}{11}+\dfrac{9}{11}\right)=\dfrac{5}{7}\times1=\dfrac{5}{7}\)
\(f3.6\times\left(1.25+8.75\right)=3.6\times10=36\)
KT
1
TD
7
TM
20 tháng 5 2016
Từ 1->100 có:100-1+1=100 (thừa số)
Mà \(\frac{1}{2};\frac{3}{4};\frac{5}{6};.....;\frac{99}{100}\) là những p/s có tử và mẫu là 2 số liên tiếp
=>từ \(\frac{1}{2}\rightarrow\frac{99}{100}\) có : 50 thừa số
=>M có 50 thừa số
Từ 2->101 có:101-2+1=100 (thừa số)
=>từ \(\frac{2}{3}\rightarrow\frac{100}{101}\) có: 50 thừa số
=>N có 50 thừa số
Do đó mỗi biểu thức M,N đều có 50 thừa số
Mà \(\frac{1}{2}< \frac{2}{3};\frac{3}{4}< \frac{4}{5};......;\frac{99}{100}< \frac{100}{101}\)
=>\(M=\frac{1}{2}.\frac{2}{3}.......\frac{99}{100}< N=\frac{2}{3}.\frac{4}{5}.........\frac{100}{101}\)
Vậy M<N
DQ
0
HL
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
28 tháng 8 2020
A=2(1-3)+4(5-3)+ 6(5-7)+...+50(49-57)
A=-4-8-12-...-100 = -(4+8+12+...+100) (tính tổng cấp số cộng)
TH
0
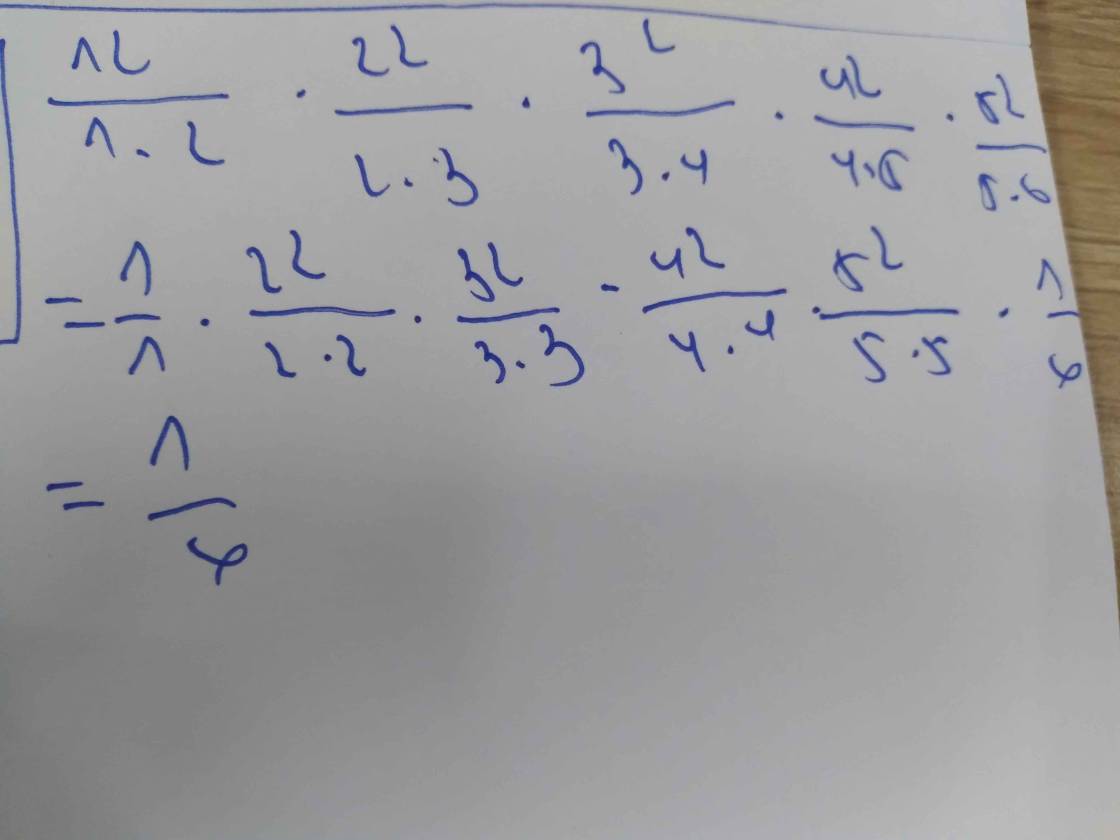
Sửa đề: -103/51*52
\(D=\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{50}+\dfrac{1}{51}-\dfrac{1}{51}-\dfrac{1}{52}\)
=1/2-1/52
=26/52-1/52=25/52