
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 8:
a) Ta có: \(A=\left(x-y\right)^3+3xy\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2-2xy+y^2+3xy\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=x^3-y^3\)
b) Ta có: \(B=\left(x+y\right)^3+3\left(x-y\right)\left(x+y\right)^2+3\left(x-y\right)^2\left(x+y\right)+\left(x-y\right)^3\)
\(=\left(x+y+x-y\right)^3\)
\(=\left(2x\right)^3=8x^3\)

1: \(=\left(y-1\right)^2\)
2: \(=\left(x+1+5\right)\left(x+1-5\right)=\left(x+6\right)\left(x-4\right)\)
3: =(1-2x)(1+2x)
\(=\left(2-3x\right)\left(4+6x+9x^2\right)\)
5: \(=\left(x+3\right)^3\)
6: \(=\left(2x-y\right)^3\)


Ta có : |x - 2| ; |x - 5| ; |x - 18| ≥0∀x∈R≥0∀x∈R
=> |x - 2| + |x - 5| + |x - 18| ≥0∀x∈R≥0∀x∈R
=> D có giá trị nhỏ nhất khi x = 2;5;18
Mà x ko thể đồng thời nhận 3 giá trị
Nên GTNN của D là : 16 khi x = 5 ok nha bạn
x^2/x-1 = x^2-4x+4/x-1 + 4 = (x-2)^1/x-1 + 4 >= 4
Dấu "=" xảy ra <=> x-2 = 0 <=> x = 2 (tm)
Vậy GTNN của x^2/x-1 = 4 <=> x= 2
k mk nha
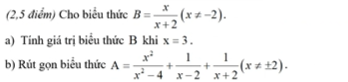

 Mọi người cứu em, tối nay phải nộp rồi.
Mọi người cứu em, tối nay phải nộp rồi.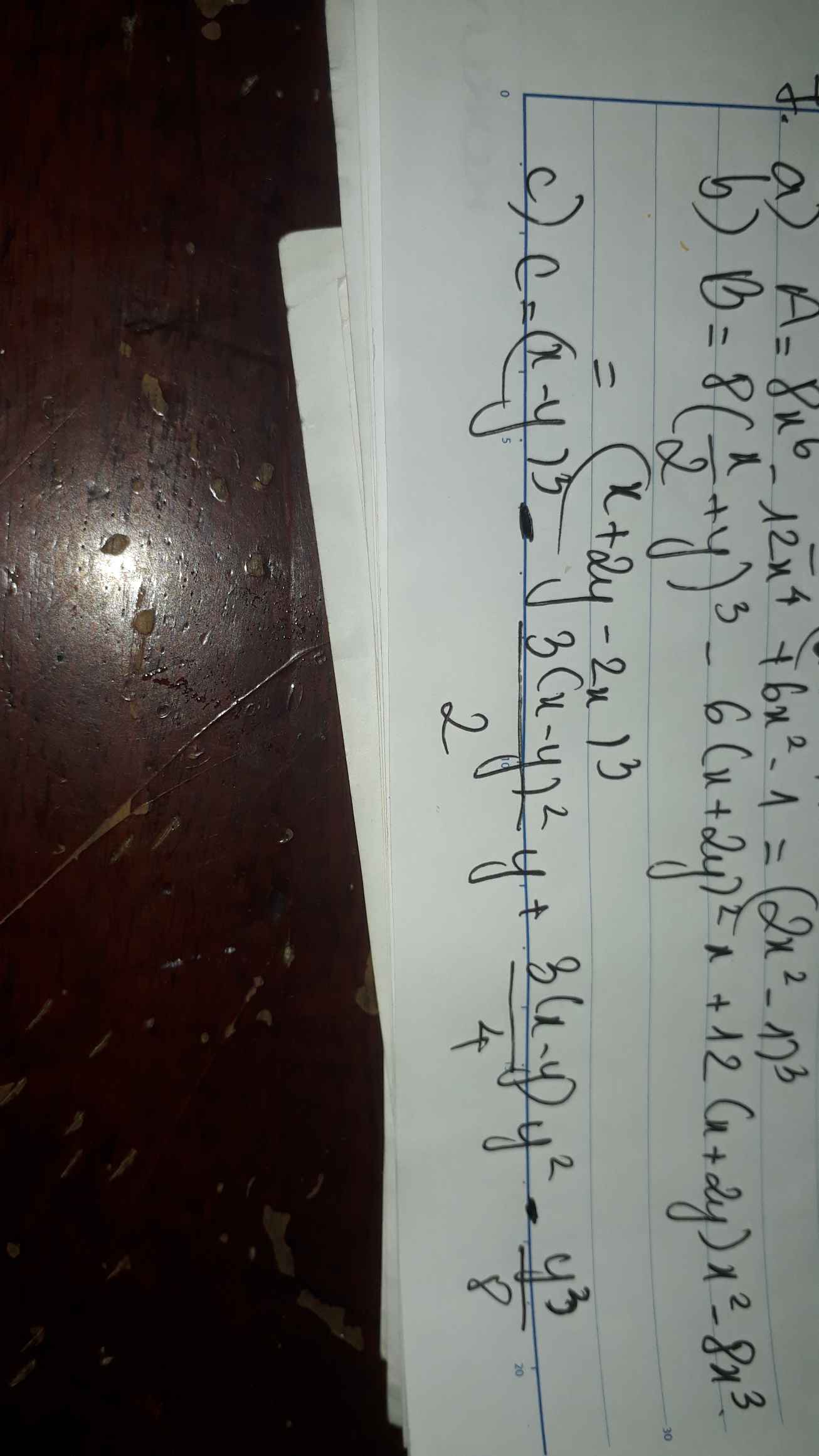

 Giúp mk với mọi người ơi mk đang cần gấp cảm ơn mọi người nhé
Giúp mk với mọi người ơi mk đang cần gấp cảm ơn mọi người nhé
a.
\(x=3\Rightarrow B=\dfrac{3}{3+2}=\dfrac{3}{5}\)
b.
\(A=\dfrac{x^2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+x+2+x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+2x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{x}{x-2}\)