Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Phương pháp.
Chia ra các khả năng có thể có của học sinh các lớp. Tính số cách chọn có thể có của mỗi trường hợp này. Lấy tổng kết quả các khả năng ở trên lại.
Lời giải chi tiết.
Ta xét các trường hợp sau.
Có 1 học sinh lớp 12C có 2 học sinh lớp 12B và 2 học sinh lớp 12A khi đó ta có 2 C 3 2 C 4 2 = 36
cách chọn.
Có 1 học sinh lớp 12C có 3 học sinh lớp 12B và 1 học sinh lớp 12A khi đó ta có 2 C 3 3 C 4 1 = 8 cách chọn.
Có 1 học sinh lớp 12C có 1 học sinh lớp 12B và 3 học sinh lớp 12A khi đó ta có 2 C 3 1 C 4 3 = 24 cách chọn.
Có 2 học sinh lớp 12C có 1 học sinh lớp 12B và 2 học sinh lớp 12A khi đó ta có C 3 1 C 4 2 = 18 cách chọn.
Có 2 học sinh lớp 12C có 2 học sinh lớp 12B và 1 học sinh lớp 12A khi đó ta có C 3 2 C 4 1 = 12 cách chọn.
Vậy tổng số cách chọn là 36 + 8 + 24 + 18 + 12 = 98
Đáp án A
Chọn 5 học sinh từ đội văn nghệ của nhà trường, ta xét các trường hợp
TH1.1 học sinh lớp 12A, 2 học sinh lớp 12B và 2 học sinh lớp 12C
⇒ có C 4 1 . C 3 2 . C 2 2 = 12 cách
TH2.2 học sinh lớp 12A, 1 học sinh lớp 12B và 2 học sinh lớp 12C
⇒ có C 4 3 . C 3 1 . C 2 2 = 18 cách
TH3.3 học sinh lớp 12A, 1 học sinh lớp 12B và 1 học sinh lớp 12C
⇒ có C 4 3 . C 3 1 . C 2 1 = 24 cách
TH4. 1 học sinh lớp 12A, 3 học sinh lớp 12B và 1 học sinh lớp 12C
⇒ có C 4 1 . C 3 3 . C 2 1 = 8 cách
TH5. 2 học sinh lớp 12A, 2 học sinh lớp 12B và 1 học sinh lớp 12C
⇒ có C 4 2 . C 3 2 . C 2 1 = 36 cách
Chọn B
TH1: Nhóm có đúng 3 học sinh có 
cách chọn
TH2: Nhóm có đúng 4 học sinh có 
cách chọn
TH3: Nhóm có đúng 5 học sinh có 
cách chọn
TH4: Nhóm có đúng 6 học sinh có 
cách chọn
TH5: Nhóm có đúng 7 học sinh có 
cách chọn
TH6: Nhóm có đúng 8 học sinh có 
cách chọn
TH7: Nhóm có đúng 9 học sinh có 
cách chọn
Vậy tổng số có 24 + 72 + 98 + 76 + 35 + 9 + 1 = 315 cách.
Chọn 3 học sinh lớp 12 có 
cách
Chọn 1 học sinh lớp 11 có 
cách
Chọn 1 học sinh lớp 10 có 
cách.
Do đó có 
cách chọn.
Chọn B.
[Số cách chọn 4 em sao cho thuộc không quá 2 trong 3 lớp] = [Số cách chọn 4 em trong 12 em] - [số cách chọn mà mỗi lớp có ít nhất 1 em]
Mà:
[Số cách chọn 4 em trong 12 em] = \(C^4_{12}=\frac{12!}{4!\left(12-4\right)!}=495\)
[số cách chọn mà mỗi lớp có ít nhất 1 em] = [Số cách chọn lớp A có 2 hs, lớp B, C mỗi lớp có 1 hs] + [Số cách chọn lớp B có 2 hs, lớp A, C mỗi lớp có 1 hs] + [Số cách chọn lớp C có 2 hs, lớp A, B mỗi lớp có 1 hs]
= \(C^2_5.C^1_4.C^1_3+C^1_5.C^2_4.C^1_3+C^1_5.C^1_4.C^2_3\)
= 120 + 90 + 60
= 270
Vậy [Số cách chọn 4 em sao cho thuộc không quá 2 trong 3 lớp] = 495 - 270 =....
Chọn A
+ Chia đều 10 đội vào 2 bảng A và B có 
cách.
Do đó số phần tử của không gian mẫu là : 
+ Sắp xếp đội của lớp 10A1 và 10A2 vào 2 bảng khác nhau A và B có 2! cách.
Chọn 4 đội trong 8 đội còn lại để xếp vào bảng có đội lớp 10A1 có C 8 4 cách.
Bốn đội còn lại xếp vào bảng còn lại.
Suy ra số cách chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau là 
Gọi A là biến cố “Chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau ” thì số các kết quả thuận lợi cho biến cố A là: 
+ Xác suất cần tìm là: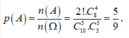 
Chọn D
Vì mỗi học sinh lớp 12A được đăng kí 1 hoặc 2 tiết mục trong số 3 tiết mục văn nghệ nên số cách lựa chọn tiết mục văn nghệ của mỗi học sinh là: C 3 1 + C 3 2 = 6.
Lớp 12A có 44 học sinh đều tham gia văn nghệ nên số cách để lớp lựa chọn là: 6 44 .