Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
+ Biên độ của vật sau mỗi nửa chu kỳ giảm 1 lượng bằng: ∆ A = 2 μ m g k = 0 , 04 m
+ Biên độ của vật sau nửa chu kì lần đầu tiên là : A’ = A - DA = 10 - 4 = 6 cm
+ Áp dụng công thức độ biến thiên cơ năng để tìm tốc độ lớn nhất của vật theo chiều âm lần đầu tiên:
A F m s = W O - W A ' = ⇔ - μ m g A ' = 1 2 m v 0 2 - 1 2 k A 2 ⇔ - 0 , 2 . 0 , 1 . 10 . 0 , 06 = 1 2 . 0 , 1 . v 0 2 - 1 2 . 10 . 0 , 06 2 → v 0 = 0 , 346 m / s
+ Biên độ của vật sau mỗi nửa chu kỳ giảm 1 lượng bằng: ∆ A = 2 μ m g k = 0 , 04 m m
+ Biên độ của vật sau nửa chu kì lần đầu tiên là : A’ = A - DA = 10 - 4 = 6 cm
+ Áp dụng công thức độ biến thiên cơ năng để tìm tốc độ lớn nhất của vật theo chiều âm lần đầu tiên:
AFms = WO - WA’
⇔ - μ m g A ' = 1 2 m v 0 2 - 1 2 k A ' 2 ⇔ - 0 , 2 . 0 , 1 . 10 . 0 , 06 = 1 2 . 0 , 1 v 0 2 - 1 2 . 10 . 0 , 06 2
=> v0 = 0,346 m/s
ü Đáp án B
Độ biến dạng của lò xo tại các vị trí cân bằng tạm Δ l 0 = μ m g k = 0 , 2.0 , 1.10 10 = 2 cm.
→ Biên độ dao động của vật ở nửa chu kì thứ hai sẽ là A 2 = 10 − 2 − 2.2 = 4 cm.
→ Tốc độ cực đại v m a x = ω A = 40 cm/s
Đáp án C
Hướng dẫn:
+ Vật m 2 sẽ rời khỏi m 2 khi hai vật này đi qua vị trí cân bằng tạm lần đầu tiên
→ Tốc độ của vật m 2 tại vị trí này
v 0 = ω X 0 − x 0 = k m 1 + m 2 X 0 − μ m 1 + m 2 g k = 50 0 , 1 + 0 , 4 0 , 1 − 0 , 05 0 , 1 + 0 , 4 .10 50 = 0 , 95
+ Quãng đường m 2 đi được từ khi rời vật m 1 đến khi dừng lại 1 2 m 2 v 0 2 = μ m 2 g S → S = v 0 2 2 μ g = 0 , 9025 m
→ Vậy tổng thời gian từ khi thả vật m 2 đến khi m 2 dừng lại là t = T 4 + 2 S μ g = 2 , 056 s
Đáp án C
Hướng dẫn: Chọn đáp án A
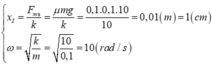
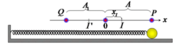
Lần 1 qua I thì I là tâm dao động với biên độ so với I:
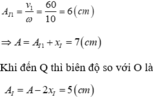
Tiếp theo thì I’ là tâm dao động và biên độ so với I’ là
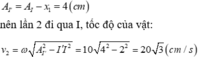
Tiếp đến vật dừng lại ở điểm cách O một khoảng
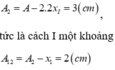
và lúc này I là tâm dao động nên lần thứ 3 đi qua I nó có tốc độ:
Chú ý: Giả sử lúc đầu vật ở O ta truyền cho nó một vận tốc để đến được tối đa là điểm . Độ giảm cơ năng đúng bằng công của lực ma sát
Giải thích: Đáp án B
Phương pháp: Vận tốc ở VTCB: v = ωA
Cách giải:
Khi về đến VTCB thì cả hai vật có vận tốc 
Sau đó vật m sẽ dao động với chu kỳ 
và biên độ 
Vật M sẽ tiếp tục chuyển động thẳng đều với vận tốc V0
Ở thời điểm lò xo có chiều dài cực đại lần đầu tiên m đến vị trí biên A’, còn M đi được quãng đường là 
=> Khoảng cách giữa hai vật m và M là:d = S - A’=4,19cm.
Chọn đáp án B.
Do không thay đổi về k, m => ω không đổi.
→ ω = k m = 20 0 , 2 = 10 π ( r a d / s ) .
Ta có năng lượng truyền cho vật là:
E t r u y e n = 1 2 m v 2 = 1 2 .0 , 2.1 2 = 0 , 1 ( J )
⇒ 1 2 k A 2 = E t r u y e n = 0 , 1 ⇒ A = 0 , 1 ( m )
Khi tới biên A lần đầu, năng lượng còn lại là:
=> Biên độ còn lại:
Hướng dẫn:
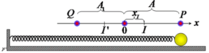
Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 2.0 , 1.10 10 = 2 cm.
→ Vật chuyển động theo chiều âm tương ứng với dao động của vật ở nửa chu kì thì hai với biên độ:
A 2 = X 0 – 3 x 0 = 10 – 3 . 2 = 4 c m
→ Tốc độ cực đại của vật trong nửa chu kì này là v m a x = ω A 2 = 40 c m / s .
Đáp án B