
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA tại C
=>CB\(\perp\)AF tại C
Xét tứ giác BHCF có \(\widehat{BHF}=\widehat{BCF}=90^0\)
nên BHCF là tứ giác nội tiếp
=>B,H,C,F cùng thuộc một đường tròn
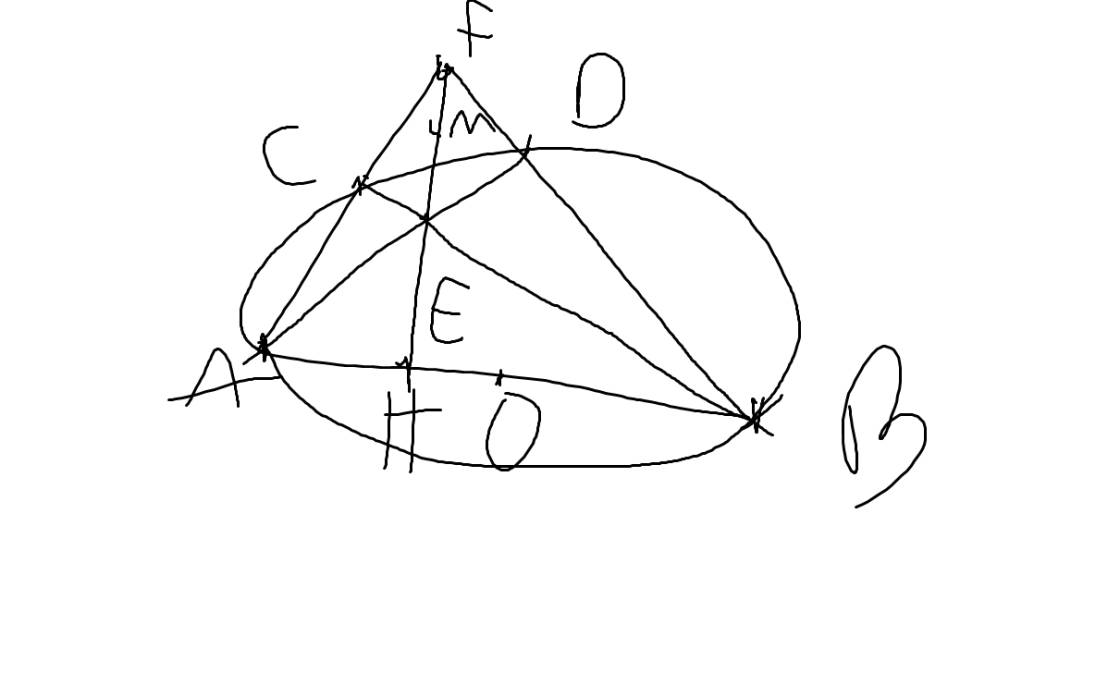

a:
Gọi O là trung điểm của AD
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó:ΔACD vuông tại C
Xét tứ giác EFDC có \(\widehat{EFD}+\widehat{ECD}=90^0+90^0=180^0\)
nên EFDC là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{BCA}\) là góc nội tiếp chắn cung BA
\(\widehat{BDA}\) là góc nội tiếp chắn cung BA
Do đó: \(\widehat{BCA}=\widehat{BDA}\)
mà \(\widehat{BDA}=\widehat{ACF}\)(ECDF là tứ giác nội tiếp)
nên \(\widehat{BCA}=\widehat{ACF}\)
=>CA là phân giác của góc BCF


a: Ta có: AD=BC
mà BC=15cm
nên AD=15cm
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AB^2+AD^2\)
\(\Leftrightarrow BD^2=15^2+8^2=289\)
hay BD=17(cm)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABD vuông tại A có AH là đường cao ứng với cạnh huyền BD, ta được:
\(AH\cdot BD=AB\cdot AD\)
\(\Leftrightarrow AH=\dfrac{8\cdot15}{17}=\dfrac{120}{17}\left(cm\right)\)

a: góc AEB=góc AHB=90 độ
=>ABHE nôi tiếp
b: Gọi N là trung điểm của AB
=>AN=HN=EN=BN
MN là đường trung bình của ΔABC
=>MN//AC
HE vuông góc AC
=>HE vuông góc MN
=>MN là trung trực của HE
=>ME=MH

1:
Ta có: ΔABC vuông tại C
mà ΔCAB nội tiếp (O)
nên O là trung điểm của AB
Xét tứ giác OBDC có \(\widehat{OBD}+\widehat{OCD}=90^0+90^0=180^0\)
nên OBDC là tứ giác nội tiếp
=>O,B,D,C cùng thuộc một đường tròn
Xét (O) có
DC,DB là các tiếp tuyến
Do đó: DC=DB
=>D nằm trên đường trung trực của CB(1)
Ta có: OC=OB
=>O nằm trên đường trung trực của CB(2)
Từ (1) và (2) suy ra OD là đường trung trực của CB
=>OD\(\perp\)CB
Ta có: AC\(\perp\)CB
CB\(\perp\)OD
Do đó: OD//AC
2: Xét (O) có
ΔBEA nội tiếp
AB là đường kính
Do đó: ΔBAE vuông tại E
=>BE\(\perp\)EA tại E
=>BE\(\perp\)AD tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(DE\cdot DA=DB^2\left(3\right)\)
Xét ΔDOB vuông tại B có BH là đường cao
nên \(DH\cdot DO=DB^2\)(4)
Từ (3) và (4) suy ra \(DE\cdot DA=DH\cdot DO\)

em xin ý kiến của thầy cô cùng những khoá anh chị đi trước ạ. Em làm bài tốt nhưng lúc về mới phát hiện 😔😔😔 .

a: Xét ΔOCD có OC=OD và \(\widehat{COD}=90^0\)
nên ΔOCD vuông cân tại O
b: \(\widehat{COD}=90^0\)
=>sđ cung nhỏ CD=90 độ
sđ cung lớn CD là: 360-90=270 độ
ΔOCD vuông tại O
=>\(CD^2=OC^2+OD^2=2R^2\)
=>\(CD=R\sqrt{2}\)

a: Xét ΔOMN có OM=ON và góc MON=60 độ
nên ΔOMN đều
b: góc MON=60 độ
=>sđ cung nhỏ MN=60 độ
sđ cung lớn MN là:
360-60=300 độ





 có vẽ hình lun ạ
có vẽ hình lun ạ
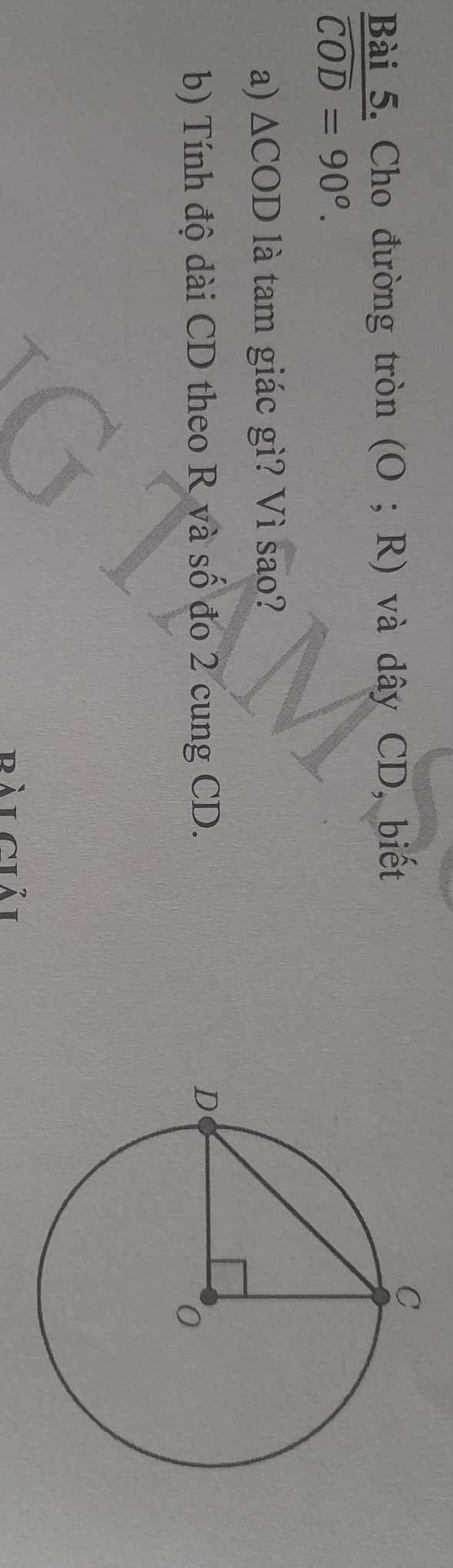

a: Xét (O) có
ΔAKB nội tiếp
AB là đường kính
Do đó: ΔAKB vuông tại K
Xét tứ giác EMBK có \(\widehat{EMB}+\widehat{EKB}=90^0+90^0=180^0\)
nên EMBK là tứ giác nội tiếp
b: Xét (O) có
OA là bán kính
OA\(\perp\)CD tại M
Do đó: \(sđ\stackrel\frown{AC}=sđ\stackrel\frown{AD}\)
Xét (O) có
\(\widehat{AKC}\) là góc nội tiếp chắn cung AC
\(\widehat{ACD}\) là góc nội tiếp chắn cung AD
\(sđ\stackrel\frown{AD}=sđ\stackrel\frown{AC}\)
Do đó: \(\widehat{AKC}=\widehat{ACD}\)
Xét ΔAKC và ΔACE có
\(\widehat{AKC}=\widehat{ACE}\)
\(\widehat{KAC}\) chung
Do đó: ΔAKC đồng dạng với ΔACE
=>\(\dfrac{AK}{AC}=\dfrac{AC}{AE}\)
=>\(AE\cdot AK=AC^2\)