Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chia lăng trụ ABD.A'B'D' thành ba tứ diện DABD', A'ABD', A'B'BD'. Phép đối xứng qua (ABD') biến DABD' thành A'ABD', Phép đối xứng qua (BA'D') biến A'ABD' thành A'B'BD' nên ba tứ diện DABA', A'ABD', A'B'BD' bằng nhau
Làm tương tự đối với lăng trụ BCD.B'C'D' ta sẽ chia được hình lập phương thành sáu tứ diện bằng nhau.

Đáp án C.
Gọi x là chiều dài đoạn thép thứ nhất, 0 < x < 10
⇒ Cạnh hình tứ diện là x 6 (tứ diện là đều)
⇒ Cạnh hình lập phương là 10 - x 12
Diện tích xung quanh của tứ diện là S 1 = 4 . 1 2 . x 6 2 . 60 °
Diện tích xung quanh của lập phương là S 2 = 6 10 - x 12 2
Tổng S 1 + S 2 đạt giá trị nhỏ nhất khi x = 5 6 2 3 36 + 1 24 = 30 2 3 + 3 = 20 3 - 30
⇒ a = 20 3 - 30 6 ; b = 10 - 20 3 + 30 12 ⇒ a + b = - 5 + 5 3 3

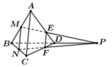
Do E, F lần lượt là trọng tâm các tam giác ABP, BCP nên
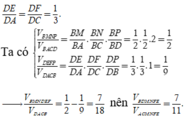
Chọn B.

Chọn đáp án A.

Chú ý: Tứ diện đều chỉ là trường hợp đặc biệt của một số tứ diện hoặc một hình chóp tam giác. Chúng ta có các kết quả như sau:
1. Cho khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng b. Thể tích khối chóp tam giác đều bằng
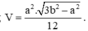
2. Cho khối tứ diện ABCD có và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là ![]()
3. Cho khối tứ diện ABCD có AB = x, CD = y và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là
![]()
4. Cho khối tứ diện gần đều ABCD có AB = CD = a, AC = BD = b, AD = BC = c. Thể tích khối tứ diện ABCD là
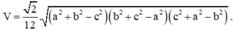

Đáp án B
Gọi tâm O, O’ lần lượt là tâm của ABCD, A’B’C’D’. Ta có I = A K ∩ O O '
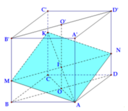
Qua I ta kẻ đường thẳng d song song BD cắt BB', DD' lần lượt tại M, N . Mặt phẳng α chính là mặt phẳng (KMAN) chia khối lập phương thành 2 phần.
Ta có 2 phần khối đa diện đối xứng qua (AA'C'C) nên ta chỉ cần xét một nửa thể tích của mỗi phần như sau:
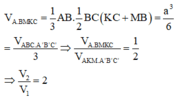
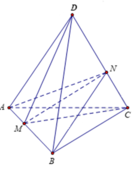
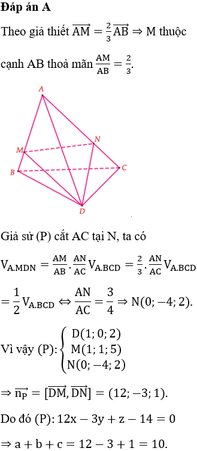
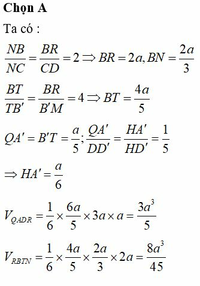
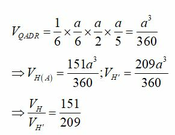
Đáp án là D
Trước hết , ta chia khối lập phương thành hai khối lăng trụ bằng nhau ABD.A'B'D' và BCD.B'C'D' vì chúng đối xứng qua mặt phẳng (BDD'B').
Trong lăng trụ ABD.A'B'D' ta xét ba khối lăng trụ D'A'AB, D'A'B'B, D'ABD ta có: D'A'AB và D'A'B'B bằng nhau vì đối xứng qua mặt phẳng (A'D'C'B).
D'A'AB và D'DAB bằng nhau vì đối xứng qua (ABC'D').
Tương tự, ta cũng chia hình lăng trụ BCD.B'C'D' thành 3 khối tứ diện D'B'BC', D'BC'C, D'BDC. Các khối tứ diện này bằng nhau và bằng ba khối tứ diện trên.