Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Với 4 y - y - 1 + y + 3 2 ≤ 8 , xét từng TH phá giá trị tuyệt đối, ta tìm được nghiệm - 3 ≤ y ≤ 0 .
Khi đó 3 x 2 - 2 x - 3 - log 3 5 = 3 x 2 - 2 x - 3 3 log 3 5 = 3 x 2 - 2 x - 3 5 ≥ 1 5 và y ∈ - 3 ; 0 ⇔ y + 4 ∈ 1 ; 4 ⇒ 5 - y + 4 ≤ 5 - 1 = 1 5 .
Do đó 3 x 2 - 2 x - 3 - log 3 5 = 5 - y + 4 ⇔ [ x = - 1 x = 3 y = - 3 ⇒ x ; y = - 1 ; - 3 ; 3 ; - 3 .
Vậy có tất cả hai cặp số thực (x;y) thỏa mãn yêu cầu bài toán.

Ta có: \(2^{x+1}.\left(-3\right)^y=12^x\)
\(\Rightarrow2^{x+1}.\left(-3\right)^y=\left(3.4\right)^x\)
\(\Rightarrow2^{x+1}.\left(-3\right)^y=3^x.4^x\)
\(\Rightarrow2^{x+1}.\left(-3\right)^y=3^x.2^{2x}\)
\(\Rightarrow2^{x+1}.\left(-1\right)^y.3^y=3^x.2^{2x}\)
\(\Rightarrow\left[{}\begin{matrix}x+1=2x\\x=y\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=y=1\end{matrix}\right.\)
Vậy x=1 , y=1

Đáp án A
Ta có e 2 x + y + 1 - e 3 x + 2 y = x + y + 1 ⇔ e 2 x + y + 1 + 2 x + y + 1 = e 3 x + 2 y + 3 x + 2 y *
Xét f t = e t + t là hàm số đồng biến trên ℝ mà f 2 x + y + 1 = f 3 x + 2 y ⇒ y = 1 - x
Khi đó log 2 2 2 x + y - 1 - m + 4 log 2 x + m 2 + 4 = 0
Phương trình (1) có nghiệm khi và chỉ khi ∆ = m + 4 - 4 m 2 + 4 ≥ 0 ⇔ 0 ≤ m ≤ 8 3 .


Chọn đáp án A
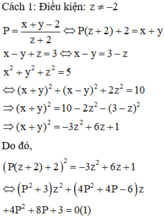

Do đó, P có thể nhận các giá trị nguyên là 0; -1
STUDY TIP |
Trong biểu thức P vai trò của z khác x, y do đó, ta tìm cách rút x, y theo z từ điều kiện ban đầu. Từ đó quy về phương trình ẩn z và tìm điều kiện để phương trình có nghiệm |

Phương trình (2), (3) là các phương trình mặt phẳng
Hai mặt phẳng này cắt nhau theo giao tuyến d có vecto chỉ phương là

Phương trình (4) là phương trình mặt cầu (S) có tâm O(0;0;0) bán kính R = 5
X, y, z tồn tại khi và chỉ khi d cắt (S)

Do đó P có thể nhận các giá trị nguyên là 0; -1
STUDY TIP |
Các biểu thức liên hệ giữa x, y, z có dạng phương trình mặt phẳng, mặt cầu. Từ đó giúp ta nghĩ đến việc xét vị trí tương dối giữa mặt cầu, với đường thẳng và mặt phẳng |

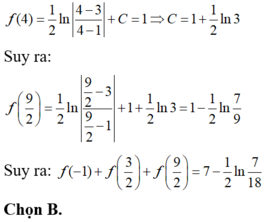

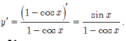
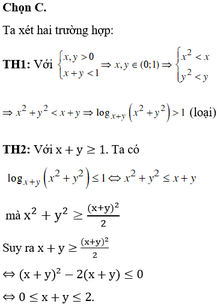
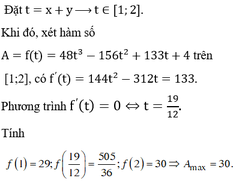

Đáp án là B