Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên mặt phẳng cho n > = điểm sao cho khoảng cách giữa 2 điểm bất kì đôi một khác nhau. Người ta nối mỗi điểm với điểm gần nhất.
CMR qua mỗi điểm co không quá 5 đoạn thẳng

Do số tam giác được lập từ n điểm đã cho là hữu hạn nên tồn tại 1 tam giác ABC có diện tích lớn nhất.
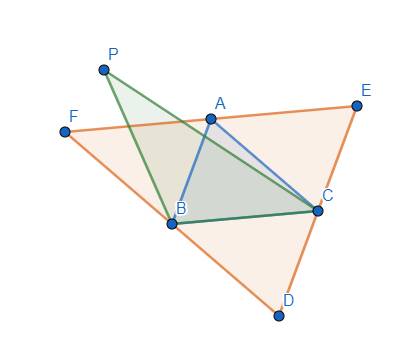
Dựng tam giác DEF sao cho A, B, C lần lượt là trung điểm của EF, DF, DE. Khi đó vì \(S_{ABC}\le1\) nên \(S_{DEF}\le4\). Ta sẽ chứng minh tam giác DEF chính là tam giác cần tìm.
Thật vậy, giả sử tồn tại điểm P trong số n điểm đã cho nằm ngoài tam giác DEF. Không mất tính tổng quát, giả sử P nằm khác phía BC đối với EF. Khi đó khoảng cách từ P đến BC sẽ lớn hơn khoảng cách từ A đến BC, dẫn đến \(S_{PBC}>S_{ABC}\), điều này là vô lí vì ta đã giả sử tam giác ABC là tam giác có diện tích lớn nhất trong số các tam giác tạo thành từ n điểm đã cho \(\Rightarrow\) tam giác DEF thỏa ycbt
Vậy ta có đpcm.
,
Nếu bạn không xem được phần trả lời của mình thì vào trang cá nhân của mình xem nhé, tại câu trả lời của mình có vẽ hình nên nó không đăng lên được ngay.

bài này dùng nguyên lý drichlet toán rời rạc
Giả sử từ điểm A trong 17 điểm đã cho nối với 16 điểm còn lại bằng 3 loại màu => Theo nguyên lý Dirichlet có ít nhất 6 đoạn thẳng cùng một màu, giả sử đó là các đoạn thẳng AB1; AB2; …;AB6 cùng được tô màu đỏ.
Nếu có 2 trong 6 điểm B1; B2; ..; B6 được nối với nhau bằng màu đỏ thì bài toán được chứng minh. Nếu không có 2 điểm nào được nối với nhau bằng màu đỏ thì 6 điểm này được nối với nhau bằng hai màu xanh hoặc vàng.
Từ điểm B1 ta nối với 5 điểm còn lại Þ Có 5 đoạn thẳng mà chỉ có 2 màu => Theo nguyên lý Diricle có ít nhất 3 đoạn thẳng cùng màu, giả sử đó là 3 đoạn thẳng B1B2, B1B3, B1B4 có cùng màu xanh.
Xét tam giác B2B3B4
TH1: nếu 3 cạnh của tam giác này cùng màu thì bài toán đã được giải xong.
TH2: 3 cạnh của tam giác không cùng màu thì sẽ có ít nhất 1 cạnh có màu xanh giả sử đó là cạnh B2B3 => Tam giác B1B2B3 có ba cạnh cùng màu xanh.
Vậycó đpcm


Xét điểm thứ nhất (A)(A) nối với 5 điểm còn lại (B,C,D,E,FB,C,D,E,F) tạo thành 5 đoạn thẳng
Vì mỗi đoạn thẳng được tô chỉ màu đỏ hoặc xanh, nên theo nguyên lí Dirichlet có ít nhất ba trong năm đoạn nói trên cùng màu. Giả sử 3 đoạn cùng màu là đoạn AB,AC,AD có 2 trường hợp:
Đoạn AB,AC,ADAB,AC,AD màu xanh tạo thành ΔABC,ABD,BCD,ABDΔABC,ABD,BCD,ABD có đỉnh thuộc cạnh màu xanh
Nếu ngược lại 3 đoạn màu đỏ thì tạo thành ΔABC,ABD,BCD,ABDΔABC,ABD,BCD,ABD có đỉnh thuộc cạnh màu đỏ.
Vậy ta có điều phải chứng minh.
Xét điểm thứ nhất (A)(A) nối với 5 điểm còn lại (B,C,D,E,FB,C,D,E,F) tạo thành 5 đoạn thẳng
Vì mỗi đoạn thẳng được tô chỉ màu đỏ hoặc xanh, nên theo nguyên lí Dirichlet có ít nhất ba trong năm đoạn nói trên cùng màu. Giả sử 3 đoạn cùng màu là đoạn AB,AC,AD có 2 trường hợp:
Đoạn AB,AC,ADAB,AC,AD màu xanh tạo thành ΔABC,ABD,BCD,ABDΔABC,ABD,BCD,ABD có đỉnh thuộc cạnh màu xanh
Nếu ngược lại 3 đoạn màu đỏ thì tạo thành ΔABC,ABD,BCD,ABDΔABC,ABD,BCD,ABD có đỉnh thuộc cạnh màu đỏ.
Vậy ta có điều phải chứng minh.