
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

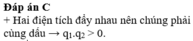

Đúng cái dạng vừa nói xong luôn :)
a/ Ta có q1 và q2 trái dấu nên q0 sẽ nằm ngoài khoảng AB và gần điện tích có độ lớn nhỏ hơn < làm sao giờ ta, tui đang ko có máy tính để tính được nên cậu tự làm nhé, có gì ko hiểu thì hỏi tui>
b/ \(\frac{\sqrt{\left|q_0\right|}}{AC}=\frac{\sqrt{\left|q_2\right|}}{AB}\Rightarrow q_0=...\)
Xác định dấu thì: \(\left|q_1\right|< \left|q_2\right|\Rightarrow\) q0 trai dau q1
\(\left|q_1\right|>\left|q_2\right|\Rightarrow\) q0 trai dau q2

1)lực tĩnh điện đẩy nhau cảu A và B là :
9*10^(9)*((1.8*10^(-8)*5.4*10^(-9))/0.03^(2))=9.72*10^(-4) N
gọi X là q c
vì tổng lục tĩnh điện tác dụng lên A ss with BC nên
ta có pt
9.72*10^(-4)+(9*10^(9)*((1.8*10^(-8)*X)/0.04^(2))=9*10^(9)*((5.4*10^(-9)*X)/0.056(2))
giải tìm được X=-1.8*10^(-8)
không chắc đúng đâu !
hình như sai cái gì đó chổ pt thay 0.05^(2) =>0.5^(2)
ta được X=-9.6*10^(-9)

Chọn đáp án C
? Lời giải:
+ Vì q1 và q2 đẩy nhau nên chúng cùng dấu. Vậy q1q2 > 0

Để \(\overrightarrow{E_M}=\overrightarrow{E}_1+\overrightarrow{E}_2=\overrightarrow{0}\) thì M phải thỏa mãn 2 điều kiện sau:
\(\left\{{}\begin{matrix}\overrightarrow{E_1}\uparrow\downarrow\overrightarrow{E_2}\left(1\right)\\E_1=E_2\left(2\right)\end{matrix}\right.\)
(1) Để hai véc tơ E1 và E2 song song ngược chiều thì M nằm trên đường thẳng nối hai điện tích, nằm ngoài hai điện tích.
(2) Để \(E_1=E_2\Rightarrow\frac{r_1}{r_2}=\sqrt{\frac{\left|Q_1\right|}{\left|Q_2\right|}}=2\Rightarrow r_1=2r_2\Rightarrow r_1>r_2\)
Dựa vào hình vẽ ta có \(r_1=r_2+8\Rightarrow r_2=8cm;r_1=16cm\)