Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điện tích q 1 tác dụng lên q 0 lực F 1 → , điện tích q2 tác dụng lên q 0 lực F 2 → .
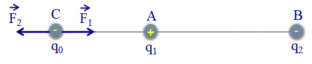
Để q0 nằm cân bằng thì F 1 → + F 2 → = 0 → ð F 1 → = - F 2 → ð F 1 → và F 2 → phải cùng phương, ngược chiều và bằng nhau về độ lớn. Để thỏa mãn các điều kiện này thì q0 phải đặt trên đường thẳng nối A, B (để hai lực cùng phương), đặt ngoài đoạn thẳng AB (để hai lực ngược chiều) và gần q1 hơn (để hai lực bằng nhau về độ lớn vì | q 1 | < | q 2 |).
Khi đó: k | q 1 q 0 | A C 2 = k | q 2 q 0 | ( A B + A C ) 2 ⇒ A B + A C A C = | q 2 | | q 1 | = 2
⇒ AC = 20 cm; BC = BA + AC = 40 cm.

Chọn: A
Hướng dẫn:
- Lực điện do q 1 = 2 (nC) = 2. 10 - 9 (C) và q 2 = 0,018 (μC) = 18. 10 - 9 (C) tác dụng lên điện tích q0 đặt tại điểm là F = q 0 .E = 0, suy ra cường độ điện trường tại điểm M là E = 0.
- Cường độ điện trường do q 1 và q 2 gây ra tại M lần lượt là E → 1 và E → 2 .
- Cường độ điện trường tổng hợp tại M là E → = E → 1 + E → 2 = 0, suy ra hai vectơ E → 1 và E → 2 phải cùng phương, ngược chiều, độ lớn bằng nhau E 1 = E 2 , điểm M thoả mãn điều kiện của E 1 và E 2 thì M phải nằm trên đường thẳng đi qua hai điện tích q 1 và q 2 , do q 1 và q 2 cùng dấu nên M nămg trong khoảng giữa q 1 và q 2 suy ra r 1 + r 2 = 10 (cm).
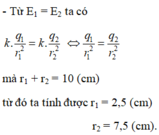

![]()
Giả sử q 0 > 0. Để q0 cân bằng thì hợp lực tác dụng lên q 0 phải bằng không, ta có:
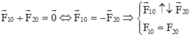
Vì q1; q2 cùng dấu nên C thuộc đoạn thẳng AB: AC + BC = AB (*) và q 1 A C 2 = q 2 B C 2 (**)
Từ (*) và (**) ta có:
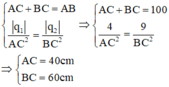

Đáp án B.
Vì q1 và q2 đặt cố định nên muốn q0 cân bằng thì ba điện tích đặt thẳng hàng, dấu “xen kẽ nhau”, q0 phải ở q0 sẽ chị tác dụng hai lực ngược hướng nhau và độ lớn bằng nhau:
k q 1 q 0 r 10 2 = k q 2 q 0 r 20 2 ⇒ r 10 = 3 r 20 ⇔ r 20 + 12 = 3 r 20 ⇒ r 20 = 6 c m
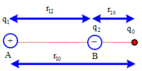



Đúng cái dạng vừa nói xong luôn :)
a/ Ta có q1 và q2 trái dấu nên q0 sẽ nằm ngoài khoảng AB và gần điện tích có độ lớn nhỏ hơn < làm sao giờ ta, tui đang ko có máy tính để tính được nên cậu tự làm nhé, có gì ko hiểu thì hỏi tui>
b/ \(\frac{\sqrt{\left|q_0\right|}}{AC}=\frac{\sqrt{\left|q_2\right|}}{AB}\Rightarrow q_0=...\)
Xác định dấu thì: \(\left|q_1\right|< \left|q_2\right|\Rightarrow\) q0 trai dau q1
\(\left|q_1\right|>\left|q_2\right|\Rightarrow\) q0 trai dau q2