

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi \(m\left(kg\right)\) là khối lượng nước bình 1 và bình 2 ban đầu.
Và \(m'\left(kg\right)\) là lượng nước được múc ra.
Khi bình 2 cân băng nhiệt, người ta múc một ca nước từ bình 2 đổ sang bình 1 và nhiệt độ bình 1 khi cân bằng nhiệt là 30. Ta có pt:
\(m\cdot c\cdot\left(30-20\right)=m'\cdot c\cdot\left(60-30\right)\Rightarrow10m=30m'\Rightarrow m=3m'\)
Nếu lặp lại một lần nữa, nhiệt độ bình 1 sau khi cân bằng là \(t\left(^oC\right):\)
\(\left(m-m'\right)\cdot c\cdot\left(60-t\right)=m'\cdot c\cdot\left(t-20\right)\)
\(\Rightarrow2\cdot\left(60-t\right)=t-20\Rightarrow t=\dfrac{140}{3}\approx46,67^oC\)

Gọi \(m\) là lượng nước chuyển đổi sau mỗi lần chuyển.
Giả sử \(t_1'\) là nhiệt độ cân bằng sau lần chuyển thứ nhất.
Gọi \(t_2'\) là nhiệt độ cân bằng sau lần chuyển thứ hai.
Sau lần chuyển thứ nhất:
Bảo toàn khối lượng: \(m_1+m=m_2-m\Rightarrow m=\dfrac{m_2-m_1}{2}=\dfrac{4-2}{2}=1kg\)
Bảo toàn nhiệt lượng: \(m_1c\left(t_1-t_1'\right)=mc\left(t_2-t_2'\right)\)
\(\Rightarrow2\cdot4200\cdot\left(20-t_1'\right)=1\cdot4200\cdot\left(60-t_2'\right)\) \((1)\)
Sau lần chuyển thứ hai:
Bảo toàn khối lượng: \(m_1+m=m_2\Rightarrow m=m_2-m_1=2kg\)
Bảo toàn nhiệt lượng: \(m_2c\left(t_2-t_2'\right)=mc\left(t_1-t_1'\right)\)
\(\Rightarrow4\cdot4200\cdot\left(60-t_2'\right)=1\cdot4200\cdot\left(30-t_1'\right)\) \((2)\)
Từ \((1)\) và \((2)\) \(\Rightarrow\left\{{}\begin{matrix}t_1'=\dfrac{130}{7}\approx18,57^oC\\t_2'=\dfrac{400}{7}\approx57,14^oC\end{matrix}\right.\)

\(Qthu\)(nước bình 2)\(=m.Cn.\left(t2-20\right)=2.4200.\left(t2-20\right)\left(J\right)\)
\(Qtoa\)(nước bình 1)\(=m1.Cn.\left(60-t2\right)=4200.m1\left(60-t2\right)\left(J\right)\)
\(=>2.4200\left(t2-20\right)=4200m1\left(60-t2\right)\)
\(=>2\left(t2-20\right)=m1\left(60-t2\right)\left(1\right)\)
*khi có cân bằng nhiệt lại rótlượng nước như cũ từ bình 2 sang bình 1. Khi đó nhiệt độ bình 1 là 580C
\(Qth\)u(nước bình 2 rót sang)\(=m1.Cn.\left(58-t2\right)=4200m1\left(58-t2\right)\)(J)
\(Qtoa\)(nuosc bình 1)\(=\left(10-m1\right).Cn.\left(60-58\right)=\left(10-m1\right).4200.2\left(J\right)\)
\(=>4200m1\left(58-t2\right)=4200\left(10-m1\right).2\)
\(=>m1\left(58-t2\right)=2\left(10-m1\right)\left(2\right)\)
\(\left(1\right)\left(2\right)\)=>hệ pt: \(\left\{{}\begin{matrix}2\left(t2-20\right)=m1\left(60-t2\right)\\m1\left(58-t2\right)=2\left(10-m1\right)\end{matrix}\right.\)
giải hệ trên \(=>\left\{{}\begin{matrix}m=\dfrac{2}{3}kg\\t2=30^oC\end{matrix}\right.\)
Vậy..............
b, có:
\(Qtoa=10.Cn.\left(60-t\right)\left(J\right)\)
\(Qthu=2.4200\left(t-20\right)\left(J\right)\)
\(=>10.4200.\left(60-t\right)=2.4200.\left(t-20\right)=>t\approx53,3^0C\)

Bạn tham khảo nhé!
a/ Giả sử khi rót lượng nước m từ bình 1 sang bình 2, nhiệt độ cân bằng của bình 2 là t nên ta có phương trình cân bằng:
m.(t - t1) = m2.(t2 - t) (1)
Tương tự lần rót tiếp theo nhiệt độ cân bằng ở bình 1 là t' = 21,950C và lượng nước trong bình 1 lúc này chỉ còn (m1 - m) nên ta có phương trình cân bằng:
m.(t - t') = (m1 - m).(t' - t1) (2)
Từ (1) và (2) ta có pt sau:
m2.(t2 - t) = m1.(t' - t1)
\(t=\dfrac{m2t2\left(t'-t1\right)}{m2}\) (3)
Thay (3) vào (2) tính toán ta rút phương trình sau:
m=m1m2(t′−t1)/m2(t2−t1)−m1(t′−t1) (4)
Thay số vào (3) và (4) ta tìm được: t = 590C và m = 0,1 Kg.
b/ Lúc này nhiệt độ của bình 1 và bình 2 lần lượt là 21,950C và 590C bây giờ ta thực hiện rót 0,1Kg nước từ bình 1 sang bình 2 thì ta có thể viết được phương trình sau:
m.(T2 - t') = m2.(t - T2)
T2=m1t′+m2t/m+m2=58,120C
Bây giờ ta tiếp tục rót từ bình 2 sang bình 1 ta cũng dễ dàng viết được phương trình sau:
m.(T1 - T2) = (m1 - m).(t - T1)
T1=mT2+(m1−m)t′/m1=23,76oC

a. Nhiệt độ cân bằng ở bình 2 và lượng nước đã rót là:
\(Q_{toa}=Q_{thu}\)
\(<=> m_2c(t_2-t)=mc(t-t_1)\)
\(<=> 4(60-t)=m(t-20)\)
\(<=> m=\dfrac{4(60-t)}{t-20}(1)\)
\(Q_{toa}=Q_{thu}\)
\(<=> mc(t-t')=(m_1-m)c(t'-t_1)\)
\(<=> m(t-21,95)=(2-m)(21,95-20)\)
\(<=> m(t-21,95)=3,9-1,95 m\)
\(<=> m(t-20)=3,9=> m=\dfrac{3,9}{t-20}(2)\)
Từ \((1)(2)\) \(=> \dfrac{4(60-t)}{t-20}=\dfrac{3,9}{t-20}\)
\(<=> 240-4t=3,9\)
\(<=> 4t=236,1=> t=59,025^oC\)
\(=> m=\dfrac{3,9}{59,025-20}=0,1kg\)
b. Nếu tiếp tục thực hiện lần thứ hai nhiệt độ cân bằng ở mỗi bình là:
\(Q_{toa}=Q_{thu}\)
\(<=> m_2c(t-t_2')=mc(t_2'-t')\)
\(<=> 4(59,025-t_2')=0,1(t_2'-21,95)\)
\(<=> t_2'=58,12^oC\)
\(Q_{toa}=Q_{thu}\)
\(<=>mc(t_2'-t_1')=(m_1-m)c(t_1'-t_1)\)
\(<=>0,1(58,12-t_1')=(2-0,1)(t_1'-21,95)\)
\(<=>t_1'=23,76^oC\)

* Tham khảo thoy nha :
Khi đổ lượng nước m từ bình 2 sang bình 1, gọi nhiệt độ cân bằng ở bình 1 là t1’. Ta có phương trình cân bằng nhiệt:
mc( t2 – t1’) = m1c ( t1’ – t1 )
<=>m( t2 – t1’ ) = m1(t1’ – t1)
Ta được: t1’ = 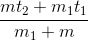 (1)
(1)
Khi đổ lượng nước m từ bình 1 sang bình 2, gọi nhiệt độ cân bằng ở bình 2 là t2’. Ta có phương trình cân bằng nhiệt: mc( t2’ – t1’ ) = ( m2 – m )c(t2 – t2’ )
<=> mt2’ – mt1’ = ( m2 – m )( t2 – t2’ )
<=> mt2’ - ( m2 – m )( t2 – t2’ ) = mt1’
Ta được: t1’ = 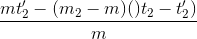 (2)
(2)
Từ (1) và (2) ta có 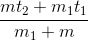 =
= 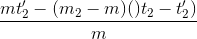
Giải phương trình trên ta được:
m=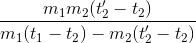 =
=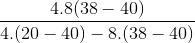 =1kg
=1kg
Thay m = 1kg vào (1) ta được: t1’ = 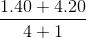 = 24oC
= 24oC

V1=5lít=>m1=5kg
V2=1lít=>m2=1kg
Gọi:
t1:nhiệt độ ban đầu của b1
t2:nhiệt độ ban đầu của b2
t'1:nhệt độ cân bằng của b1
t'2:nhiệt độ cân bằng của b2
m:lượng nước rót wa lại
Theo ptcbn:
nhlg toa ra của m nước 80*C rót từ b1wa b2=nhlg thu vào của b2
Q1=Q2
m.c.(t1-t'2)=m2.c.(t'2-t2)
m.(t1-t'2)=m2.(t'2-t2)
m.(60-t'2)=1(t'2-20) (1)
60m-mt'2=t'2-20 (2)
Theo ptcbn:
nhlg tỏa ra của fần nước còn lại trong b1=nhlg thu vao của m nước có nhiệt độ là t'2 rót từ b2 wa b1
Q'1=Q'2
(m1-m).c.(t1-t'1)=m.c.(t'1-t'2)
(m1-m).(t1-t'1)=m.(t'1-t'2)
(5-m).(60-59)=m.(59-t'2)
5-m=59m-mt'2
60m-mt'2=5 (3)
Từ (2) và (3)
=>t'2-20=5
=>t'2=25
Thế t'2=25 vào (1)
(1)<=>m.(60-25)=1.(25-20)
35m=5
=>m=5/35=1/7=0,143 kg
Vậy lượng nước rót wa rót lại gần bằng 0,143 kg