Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

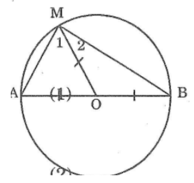
Nối OM, ta có:
OA = OM (bán kính đường tròn tâm O)
Nên ΔOAM cân tại O
⇒∠A =∠M1(tính chất tam giác cân)(1)
OM = OB (bán kính đường tròn tâm O)
Suy ra: ΔOBM cân tại O
⇒∠B =∠M2(tính chất tam giác cân) (2)
Trong ΔAMB ta có:
∠A + ∠AMB + ∠B = 180º (tổng ba góc trong tam giác)
⇒∠A +∠B +∠M1+∠M2 =180 (3)
Từ (1), (2) và (3) suy ra: 2(∠M1 + ∠M2)=180o
Vậy: ∠M1+∠M2=90o hay ∠(AMB) =90o


(h.141)\(\Delta AOM\) cân \(\Rightarrow\)\(\widehat{A}=\widehat{M1}\)
\(\Delta BOM\) cân \(\Rightarrow\)\(\widehat{B}=\widehat{M2}\)
Suy ra \(\widehat{M1}+\widehat{M2}=\widehat{A}+\widehat{B}\)do đó
\(\widehat{AMB}=\widehat{A}+\widehat{B}\).Ta lại có:
\(\widehat{AMB}+\widehat{A}+\widehat{B}=180^0\) nên
\(\widehat{AMB}=90^0\)

Ta có hình vẽ:
a/ Xét tam giác OMA và tam giác OMB có:
OM: cạnh chung
OA = OB (GT)
MA = MB (vì có cùng bán kính)
=> tam giác OMA = tam giác OMB (c.c.c)
Xét tam giác ONA và tam giác ONB có:
ON: cạnh chung
OA = OB (GT)
AN = BN (vì có cùng bán kính)
=> tam giác ONA = tam giác ONB (c.c.c)
b/ Ta có: OA = OB
AM = MB (do tam giác OMA = tam giác OBM)
AN = NB (do tam giác ONA = tam giác ONB)
=> O,M,N thẳng hàng
c/ Xét tam giác AMN và tam giác BMN có:
MN: cạnh chung
AM = MB (vì tam giác OMA = tam giác OMB)
AN = NB (vì tam giác ONA = tam giác ONB)
=> tam giác AMN = tam giác BMN (c.c.c)
d/ Ta có: tam giác AMN = tam giác BMN (câu c)
=> \(\widehat{AMN}\)=\(\widehat{BMN}\)( 2 góc tương ứng)
=> MN là phân giác của góc AMB (đpcm)
mik cũng đang định hỏi câu này nè, mai mik cũng học luôn à, cám ơn bạn nhé❤
em moi hoc lop 6 thoi chi oi