Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Gọi số cần tìm có dạng a 1 a 2 a 3 a 4 a 5 ¯
thỏa mãn a 1 > a 2 > a 3 > a 4 > a 5
và a 1 ∈ A = 0 ; 1 ; 2 ; . . . ; 9
Vì mỗi tập hợp gồm 5 chữ số thuộc tập hợp A chỉ tạo được một số thỏa yêu cầu bài toán
Vậy có C 10 5 = 252 số cần tìm
Tìm số các số nguyên dương gồm năm chữ số sao cho mỗi chữ số của số đó lớn hơn chữ số ở bên phải nó.
Có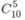 
cách chọn 5 chữ số khác nhau để lập số cần thiết. Nhưng khi đã có 5 chữ số khác nhau rồi, chỉ có một cách xếp 5 chữ số đó để tạo nên số cần thiết. Vậy có 
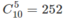số.
Có \(C^5_{10}\) cách chọn 5 chữ số khác nhau để lập số cần thiết. Nhưng khi đã có 5 chữ số khác nhau rồi, chỉ có một cách xếp 5 chữ số đó để tạo nên số cần thiết.
Vậy có \(C^5_{10}=252\) số.
3:
Ta sẽ chia M ra làm 3 nhóm
Nhóm 1: \(A=\left\{0;3;6\right\}\)
Nhóm 2: \(B=\left\{1;4;7\right\}\)
Nhóm 3: \(C=\left\{2;5;8\right\}\)
TH1: 1 số A,1 số B, 1 số C
*Nếu số ở A chọn là số 0 thì sẽ có 3*3*2*2*1=36 cách
*Nếu số A chọn khác 0 thì sẽ là 2*3*3*3!=108 cách
=>Có 108+36=144 cách
TH2: 3 số A
=>Có 2*2*1=4 số
TH3: 3 số B
=>Có 3!=6 số
TH4: 3 số C
=>Có 3!=6 số
=>Có 144+4+6+6=148+12=160 số
Chọn C
Giả sử số lập được có dạng 
Ta có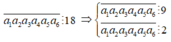 
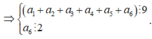
Vì 
nên ta có các trường hợp sau
Trường hợp 1:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ 
+ Có 3 cách chọn chọn a 6
+ Có 5! cách chọn chọn bộ 5 số 
Suy ra có 3.5! = 360 số.
Trường hợp 2:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ 
+
a
6
= 0, có 5! cách chọn bộ 5 số 
+
a
6
≠
0 khi đó
a
6
có 3 cách chọn,
a
1
có 4 cách chọn và có 4! cách chọn bộ 4 số 
Suy ra có 5! + 3.4.4!= 408 số
Trường hợp 3:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ 
+
a
6
= 0, có 5! cách chọn bộ 5 số 
+
a
6
≠
0 khi đó
a
6
có 1 cách chọn,
a
1
có 4 cách chọn và có 4! cách chọn bộ 4 số 
Suy ra có 5! + 1.4.4! = 216 số
Vậy có: 360 + 408 + 216 = 984 số.
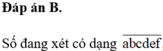
Đáp án B
Gọi số cần tìm có dạng a 1 a 2 a 3 a 4 a 5 ¯
thỏa mãn a 1 > a 2 > a 3 > a 4 > a 5
và a i ∈ A 0 ; 1 ; 2 ; . . . ; 9
Vì mỗi tập hợp gồm 5 chữ số thuộc tập hợp A chỉ tạo được một số thỏa yêu cầu bài toán
Vậy có C 10 5 = 252 số cần tìm