Có bao nhiêu số tự nhiên a sao cho lim 9 n + 3 n + 1 6 n + 9 n + 2 ≤ 1 3...

Có bao nhiêu số tự nhiên a sao cho lim 9 n + 3 n + 1 6...

QT

Quyết Thắng Đỗ

9 tháng 4 2020

*Bài tập tương tự: Tìm các giới hạn sau:

a) lim ∛(n³)-5n+9/3n-2

b) lim n³-n²-5/n⁴-2n²+1

c) lim -n³+2n²-1/n²+n-1

d) lim √(9n²+1)-2n/6n+2

e) lim 2.5ⁿ-9ⁿ⁺¹/1+9ⁿ

d) lim 1²+2²+3²+...n²/5n³-n2+1

d) lim

#Toán lớp 11

2

TH

Trần Hữu Tuyển

9 tháng 4 2020

c;Chia n³ tử dần tới -1 mẫu dần tới 0 nên lim=-\(\infty\)

Đúng(0)

TH

Trần Hữu Tuyển

9 tháng 4 2020

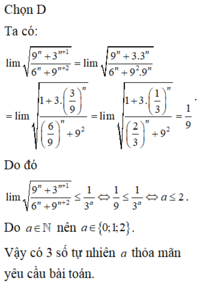
a;Chia n cả tử và mẫu

b;Chia cho n⁴ mà tử dần đến 0 mẫu dần đến 1 nên lim =0

Đúng(0)

NC

Ngoc Chau

21 tháng 4 2020

TÍNH CÁC GIỚI HẠN SAU:

a) lim n^3 +2n^2 -n +1

b) lim n^3 -2n^5 -3n-9

c)lim n^3 -2n/ 3n^2+n-2

d) lim 3n-2n^4/ 5n^2 -n +12

e) lim ( căn(2n^2 +3) - căn n^2 +1

f) lim căn( 4n^2 -3n) -2n

#Toán lớp 11

0

NC

Ngoc Chau

22 tháng 4 2020

Tính các giới hạn sau:

a) lim n^3 +2n^2 -n+1

b) lim n^3 -2n^5 -3n-9

c) lim n^3 -2n/ 3n^2 +n-2

d) lim 3n -2n^4/ 5n^2 -n+12

e) lim (căn 2n^2 +3 - căn n^2 +1)

f) lim căn (4n^2-3n). -2n

#Toán lớp 11

0

NH

Nguyễn Hải Vân

1 tháng 2 2021

a, lim \(\dfrac{\sqrt{n+1}}{1+\sqrt{n}}\)

b, lim \(\dfrac{1+2+...+n}{n^2+2}\)

c, lim \((\sqrt{n^2+n+1}-n)\)

d, lim \((\sqrt{3n-1}-\sqrt{2n-1})\)

e, lim \((\sqrt[3]{n^3+2n^2}-n)\)

g, lim \(\dfrac{(2)^{n}+(3)^{n+2}}{4×(3)^{n}+(2)^{n+3}}\)

#Toán lớp 11

1

HT

Hoàng Tử Hà

1 tháng 2 2021

a/ \(=\lim\limits\dfrac{\sqrt{\dfrac{n}{n}+\dfrac{1}{n}}}{\dfrac{1}{\sqrt{n}}+\sqrt{\dfrac{n}{n}}}=1\)

b/ \(1+2+...+n=\dfrac{n\left(n+1\right)}{2}\)

\(\Rightarrow\lim\limits\dfrac{n\left(n+1\right)}{2n^2+4}=\lim\limits\dfrac{\dfrac{n^2}{n^2}+\dfrac{n}{n^2}}{\dfrac{2n^2}{n^2}+\dfrac{4}{n^2}}=\dfrac{1}{2}\)

c/ \(=\lim\limits\dfrac{n^2+n+1-n^2}{\sqrt{n^2+n+1}+n}=\lim\limits\dfrac{n+1}{\sqrt{n^2+n+1}+n}=\lim\limits\dfrac{\dfrac{n}{n}+\dfrac{1}{n}}{\sqrt{\dfrac{n^2}{n^2}+\dfrac{n}{n^2}+\dfrac{1}{n^2}}+\dfrac{n}{n}}=\dfrac{1}{1+1}=\dfrac{1}{2}\)

d/ \(=\lim\limits\left[\sqrt{n}\left(\sqrt{3-\dfrac{1}{\sqrt{n}}}-\sqrt{2-\dfrac{1}{\sqrt{n}}}\right)\right]=\lim\limits\left[\sqrt{n}\left(\sqrt{3}-\sqrt{2}\right)\right]=+\infty\)

e/ \(=\lim\limits\dfrac{n^3+2n^2-n-n^3}{\left(\sqrt[3]{n^3+2n^2}\right)^2+n.\sqrt[3]{n^3+2n^2}+n^2}=\lim\limits\dfrac{2n^2-n}{\left(n^3+2n^2\right)^{\dfrac{2}{3}}+n.\left(n^3+2n^2\right)^{\dfrac{1}{3}}+n^2}\)

\(=\dfrac{2}{1+1+1}=\dfrac{2}{3}\)

g/ \(=\lim\limits\dfrac{2^n+9.3^n}{4.3^n+8.2^n}=\lim\limits\dfrac{\left(\dfrac{2}{3}\right)^n+9.\left(\dfrac{3}{3}\right)^n}{4.\left(\dfrac{3}{3}\right)^n+8.\left(\dfrac{2}{3}\right)^n}=\dfrac{9}{4}\)

Đúng(2)

NH

Nguyễn Hải Vân

1 tháng 2 2021

Mình cảm ơn nhiều nhé❤

Đúng(0)

H

Hobiee

4 tháng 11 2023

Tìm giới hạn dãy số :

\(a,lim\dfrac{5n+1}{2n}\\ b,lim\dfrac{6n^2+8n+1}{5n^2+3}\\ c,lim\dfrac{3^n+2^n}{4.3^n}\\ d,lim\dfrac{\sqrt{n^2+5n+3}}{6n+2}\)

#Toán lớp 11

3

NL

Nguyễn Lê Phước Thịnh

4 tháng 11 2023

a: \(\lim\limits\dfrac{5n+1}{2n}=\lim\limits\dfrac{\dfrac{5n}{n}+\dfrac{1}{n}}{\dfrac{2n}{n}}=\lim\limits\dfrac{5+\dfrac{1}{n}}{2}=\dfrac{5+0}{2}=\dfrac{5}{2}\)

b: \(\lim\limits\dfrac{6n^2+8n+1}{5n^2+3}\)

\(=\lim\limits\dfrac{\dfrac{6n^2}{n^2}+\dfrac{8n}{n^2}+\dfrac{1}{n^2}}{\dfrac{5n^2}{n^2}+\dfrac{3}{n^2}}\)

\(=\lim\limits\dfrac{6+\dfrac{8}{n}+\dfrac{1}{n^2}}{5+\dfrac{3}{n^2}}\)

\(=\dfrac{6+0+0}{5+0}=\dfrac{6}{5}\)

c: \(\lim\limits\dfrac{3^n+2^n}{4\cdot3^n}\)

\(=\lim\limits\dfrac{\dfrac{3^n}{3^n}+\left(\dfrac{2}{3}\right)^n}{4\cdot\left(\dfrac{3^n}{3^n}\right)}\)

\(=\lim\limits\dfrac{1+\left(\dfrac{2}{3}\right)^n}{4}=\dfrac{1+0}{4}=\dfrac{1}{4}\)

d: \(\lim\limits\dfrac{\sqrt{n^2+5n+3}}{6n+2}\)

\(=\lim\limits\dfrac{\sqrt{\dfrac{n^2}{n^2}+\dfrac{5n}{n^2}+\dfrac{3}{n^2}}}{\dfrac{6n}{n}+\dfrac{2}{n}}\)

\(=\lim\limits\dfrac{\sqrt{1+\dfrac{5}{n}+\dfrac{3}{n^2}}}{6+\dfrac{2}{n}}\)

\(=\dfrac{\sqrt{1+0+0}}{6}=\dfrac{1}{6}\)

Đúng(2)

AD

@DanHee

4 tháng 11 2023

\(a,lim\dfrac{5n+1}{2n}=lim\dfrac{\dfrac{5n}{n}+\dfrac{1}{n}}{\dfrac{2n}{n}}=lim\dfrac{5+\dfrac{1}{n}}{2}=\dfrac{5}{2}\\ b,lim\dfrac{6n^2+8n+1}{5n^2+3}=lim\dfrac{\dfrac{6n^2}{n^2}+\dfrac{8n}{n^2}+\dfrac{1}{n^2}}{\dfrac{5n^2}{n^2}+\dfrac{3}{n^2}}=lim\dfrac{6+\dfrac{8}{n}+\dfrac{1}{n^2}}{5+\dfrac{3}{n^2}}=\dfrac{6}{5}\)

\(c,lim\dfrac{3^n+2^n}{4.3^n}=\dfrac{\dfrac{3^n}{3^n}+\dfrac{2^n}{3^n}}{\dfrac{4.3^n}{3^n}}=\dfrac{1+\left(\dfrac{2}{3}\right)^n}{4}=\dfrac{1}{4}\)

\(d,lim\dfrac{\sqrt{n^2+5n+3}}{6n+2}=lim\dfrac{\sqrt{\dfrac{n^2+5n+3}{n^2}}}{\dfrac{6n}{n}+\dfrac{2}{n}}=lim\dfrac{\sqrt{1+\dfrac{5}{n}+\dfrac{3}{n^2}}}{6+\dfrac{2}{n}}=\dfrac{1}{6}\)

Đúng(2)

HC

Hiếu Chuối

5 tháng 1 2021

Tìm giới hạn các dãy số...

Đọc tiếp

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

5 tháng 1 2021

\(a=lim\dfrac{\left(\dfrac{2}{6}\right)^n+1-\dfrac{1}{4}\left(\dfrac{4}{6}\right)^n}{\left(\dfrac{3}{6}\right)^n+6}=\dfrac{1}{6}\)

\(b=\lim\dfrac{\left(n+1\right)^2}{3n^2+4}=\lim\dfrac{n^2+2n+1}{3n^2+4}=\lim\dfrac{1+\dfrac{2}{n}+\dfrac{1}{n^2}}{3+\dfrac{4}{n^2}}=\dfrac{1}{3}\)

\(c=\lim\dfrac{n\left(n+1\right)}{2\left(n^2-3\right)}=\lim\dfrac{n^2+n}{2n^2-6}=\lim\dfrac{1+\dfrac{1}{n}}{2-\dfrac{6}{n^2}}=\dfrac{1}{2}\)

\(d=\lim\left[1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n}-\dfrac{1}{n+1}\right]=\lim\left[1-\dfrac{1}{n+1}\right]=1\)

\(e=\lim\dfrac{1}{2}\left[1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2n-1}-\dfrac{1}{2n+1}\right]\)

\(=\lim\dfrac{1}{2}\left[1-\dfrac{1}{2n+1}\right]=\dfrac{1}{2}\)

Đúng(4)

BL

bao Le

11 tháng 12 2021

D= lim \(\dfrac{6-9^{n+2}}{3+3^n+39^{n+1}}\)

#Toán lớp 11

2

NV

Nguyễn Việt Lâm

Giáo viên

11 tháng 12 2021

Đề là \(39^{n+1}\) hay \(3.9^{n+1}\) vậy bạn?

Đúng(0)

BL

bao Le

11 tháng 12 2021

39 ạ

Đúng(0)

JE

Julian Edward

6 tháng 2 2021

Tìm các giới hạn sau:

a) \(lim\left(\sqrt{4n+1}-2\sqrt{n}\right)\)

b) \(lim\left(\sqrt{n^2+2n}-\sqrt{n^2-2n}-n\right)\)

c) \(lim\left(\sqrt{9^n-3^n}-4^n\right)\)

d) \(lim\left(3n^3+2n^2+n\right)\)

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

6 tháng 2 2021

\(a=\lim\dfrac{1}{\sqrt{4n+1}+2\sqrt{n}}=\dfrac{1}{\infty}=0\)

\(b=\lim n\left(\sqrt{1+\dfrac{2}{n}}-\sqrt{1-\dfrac{2}{n}}-1\right)=+\infty.\left(-1\right)=-\infty\)

\(c=\lim4^n\left(\sqrt{\left(\dfrac{9}{16}\right)^n-\left(\dfrac{3}{16}\right)^n}-1\right)=+\infty.\left(-1\right)=-\infty\)

\(d=\lim n^3\left(3+\dfrac{2}{n}+\dfrac{1}{n^2}\right)=+\infty.3=+\infty\)

Đúng(2)

TT

Trần Thị Ngọc Ánh 1

6 tháng 2 2021

thưa thầy câu 1 nếu rút căn n ra thì lm thế nào ạ

Đúng(0)

TN

Thư Nguyễn Huỳnh Anh

20 tháng 1 2021

...

Đọc tiếp

#Toán lớp 11

2

NV

Nguyễn Việt Lâm

Giáo viên

20 tháng 1 2021

\(a=\lim\sqrt{n^3}\sqrt{\dfrac{1}{n^3}+\dfrac{2}{n^2}-1}=\infty.\left(-1\right)=-\infty\)

\(b=\lim\left(\sqrt{n^2+2n+3}-n+n-\sqrt[3]{n^2+n^3}\right)\)

\(=\lim\dfrac{2n+3}{\sqrt{n^2+2n+3}+n}+\lim\dfrac{-n^2}{n^2+n\sqrt[3]{n^2+n^3}+\sqrt[3]{\left(n^2+n^3\right)^2}}\)

\(=\lim\dfrac{2+\dfrac{3}{n}}{\sqrt{1+\dfrac{2}{n}+\dfrac{3}{n^2}}+1}+\lim\dfrac{-1}{1+\sqrt[3]{\dfrac{1}{n}+1}+\sqrt[3]{\left(\dfrac{1}{n}+1\right)^2}}=\dfrac{2}{2}-\dfrac{1}{3}=\dfrac{2}{3}\)

\(c=\lim\dfrac{\left(\dfrac{2}{\sqrt{n}}+\dfrac{1}{n}\right)\left(\dfrac{1}{\sqrt{n}}+\dfrac{3}{n}\right)}{\left(1+\dfrac{1}{n}\right)\left(1+\dfrac{2}{n}\right)}=\dfrac{0.0}{1.1}=0\)

Đúng(1)

NV

Nguyễn Việt Lâm

Giáo viên

20 tháng 1 2021

\(d=\lim\dfrac{4-3\left(\dfrac{2}{4}\right)^n}{9.\left(\dfrac{3}{4}\right)^n+\left(\dfrac{2}{4}\right)^n}=\dfrac{4}{0}=+\infty\)

\(e=\lim\dfrac{7-25\left(\dfrac{5}{7}\right)^n+3.\left(\dfrac{1}{7}\right)^n}{12.\left(\dfrac{6}{7}\right)^n-\left(\dfrac{3}{7}\right)^n+3\left(\dfrac{1}{7}\right)^n}=\dfrac{7}{0}=+\infty\)

\(f=\lim\dfrac{n^4-4n^6}{n\left(\sqrt{n^4+1}+\sqrt{4n^6+1}\right)}=\lim\dfrac{\dfrac{1}{n^2}-6}{\sqrt{\dfrac{1}{n^6}+\dfrac{1}{n^{10}}}+\sqrt{\dfrac{4}{n^4}+\dfrac{1}{n^{10}}}}=\dfrac{-6}{0}=-\infty\)

Đúng(0)

JE

Julian Edward

8 tháng 2 2021

cho giới hạn \(lim\dfrac{1+3^n}{\sqrt{4-a^2}+a.3^n}\) (a là tham số). có bao nhiêu giá trị nguyên của a thì kq giới hạn đã cho là một số hữu hạn

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

8 tháng 2 2021

\(=\lim\dfrac{\left(\dfrac{1}{3}\right)^n+1}{\dfrac{\sqrt{4-a^2}}{3^n}+a}=\dfrac{1}{a}\)

Giới hạn đã cho là hữu hạn khi: \(\left\{{}\begin{matrix}a^2\le4\\a\ne0\end{matrix}\right.\) \(\Rightarrow a=\left\{-2;-1;1;2\right\}\)

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP