Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Cách giải: Ta có:
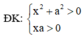
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
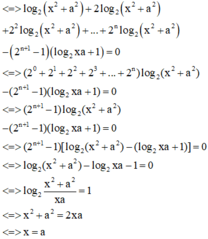
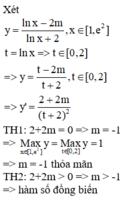
![]()
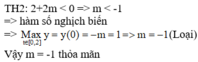

Đáp án C.
Ta có
log b a 2018 = log b a 2018 ⇔ log b a 2018 = 2018 log b a ⇔ log b a = 0 log b a 2017 = 2018
⇔ a = 1 log b a = 2018 2017 ⇔ a = 1 a = b 2018 2017
Do a là số thực dương nên với mỗi số nguyên b thỏa mãn điều kiện 2 ≤ b ≤ 200 thì sẽ tạo ra một cặp số a ; b thỏa mãn yêu cầu đề bài.
Do vậy có 2 × 200 − 2 1 + 1 = 398 cặp. Vậy ta chọn C.
Lời giải sai: log b a 2018 = 2018 log b a ⇔ log b a 2017 = 2018 , tức là bỏ mất trường hợp log b a = 0 , từ đó dẫn đến chọn đáp án B

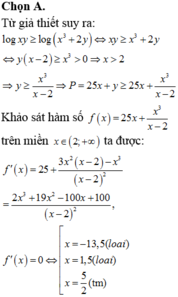
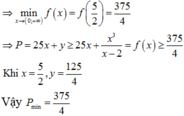
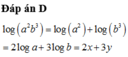
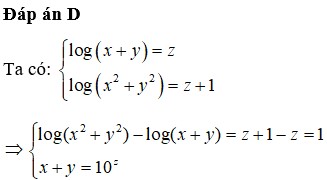
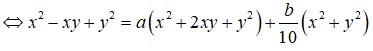
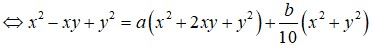
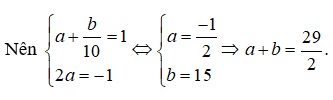
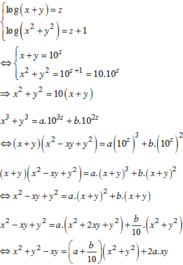
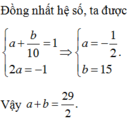

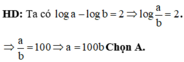
Đáp án B.
Điều kiện: x − 40 > 0 60 − x > 0 ⇔ 40 < x < 60 . Khi đó ta có:
log x − 40 + log 60 − x < 2 ⇔ log x − 40 60 − x < 2 ⇔ x − 40 60 − x < 10 2
x 2 − 100 x + 2500 > 0 ⇔ x − 50 2 > 0 ⇔ x ≠ 50
(do x − 50 2 ≥ 0 với mọi x).
Kết hợp với điều kiện ta có x ∈ 40 ; 60 \ 50 .
Suy ra có 60 − 40 − 1 − 1 = 18 số nguyên dương thỏa mãn điều kiện đã cho.
Lưu ý: Lỗi sai thường gặp: x − 50 2 > 0 ⇔ x > 50 ; x − 50 2 > 0
thỏa mãn với mọi x ∈ ℝ .