LM
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HH
21 tháng 6 2020
ABCD là hình vuông
\(\Rightarrow\widehat{AOB}=90^o\)hay \(\widehat{AOE}+\widehat{EOB}=90^o\)
Ta lại có : \(\widehat{xOy}=90^o\)hay \(\widehat{EOB}+\widehat{BOF}=90^o\)
\(\Rightarrow\widehat{AOE}=\widehat{BOF}\)( cùng phụ với \(\widehat{EOB}\))
+) Xét 2 tam giác : AOE và BOF , có :
OA = OB
\(\widehat{OAE}=\widehat{OBF}\left(=90^o\right)\)
\(\widehat{AOE}=\widehat{BOF}\left(cmt\right)\)
\(\Rightarrow\Delta AOE=\Delta BOF\left(g-c-g\right)\)
\(\Rightarrow S_{AOE}=S_{BOF}\)
\(\Rightarrow S_{AOE}+S_{OEB}=S_{BOF}+S_{OEB}\)
hay \(S_{AOB}=S_{OEBF}\)
Mà \(S_{AOB}=\frac{1}{2}S_{ABCD}=\frac{a^2}{4}\)
\(\Rightarrow S_{OEBF}=\frac{a^2}{4}\)
22 tháng 4 2021
a) Xét tứ giác ABHK có
\(\widehat{AHB}=\widehat{AKB}\left(=90^0\right)\)
\(\widehat{AHB}\) và \(\widehat{AKB}\) là hai góc cùng nhìn cạnh AB
Do đó: ABHK là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
CM
27 tháng 3 2018
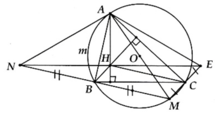
a, BH ^ AC và CM ^ AC Þ BH//CM
Tương tự => CH//BM
=> BHCM là hình bình hành
b, Chứng minh BNHC là hình bình hành
=> NH//BC
=> AH ^ NH => A H M ^ = 90 0
Mà A B N ^ = 90 0 => Tứ giác AHBN nội tiếp
c, Tương tự ý b, ta có: BHEC là hình bình hành. Vậy NH và HE//BC => N, H, E thẳng hàng
d, A B N ^ = 90 0 => AN là đường kính đường tròn ngoại tiếp tứ giác AHBN
AN = AM = 2R, AB = R 3 => A m B ⏜ = 120 0
S A O B = 1 2 S A B M = R 2 3 4
S A m B ⏜ = S a t A O B - S A O B = R 2 12 4 π - 3 3
=> S cần tìm = 2 S A m B ⏜ = R 2 6 4 π - 3 3
30 tháng 12 2019
a ) Ta có : \(\widehat{A}=\widehat{D}=\widehat{E}=90^o\left(gt\right)\)
\(\Rightarrow ADME\) là hình chữ nhật ( tứ giác có ba góc vuông )
b ) Ta có : ME là đường trung bình của tam giác ABC
\(\Rightarrow ME//AB\) và \(ME=\frac{1}{2}AB=\frac{1}{2}.6=3\left(cm\right)\)
\(\Rightarrow AD=ME=3\left(cm\right)\)( cạnh đối hình chữ nhật )
Lại có : \(\hept{\begin{cases}ME//AB\left(cmt\right)\\MB=MC\left(gt\right)\end{cases}}\)
\(\Rightarrow AE=CE=\frac{AC}{2}=\frac{8}{2}=4\left(cm\right)\)
ADME : hình chữ nhật
\(\Rightarrow A_{ADME}=AD.AE=3.4=12\left(cm^2\right)\)
c ) Dễ thấy AC là đường trung trực của MK
\(\Rightarrow AM=AK\)và \(CM=CK\)
Mà AM = CM \(\left(=\frac{1}{2}BC\right)\) ( \(\Delta ABC\) vuông tại A )
\(\Rightarrow AM=AK=CM=CK\)
\(\Rightarrow AMCK\)là hình thoi ( tứ giác có 4 cạnh bằng nhau )
d ) Ta có : \(ME=\frac{1}{2}AB\)
\(\Rightarrow AB=2ME=MK\)
Hình thoi AMCK là hình vuông \(\Leftrightarrow AC=MK\)
\(\Leftrightarrow AC=AB\) ( vì AB = MK )
\(\Leftrightarrow\Delta ABC\)cân tại A
Mà \(\Delta ABC\) vuông tại A (gt)
Vậy \(\Delta ABC\)vuông cân tại A thì hình thoi AMCK là hình vuông