Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Biến đổi hệ phương trình ban đầu ta được hệ x - y = 0 3 x + 3 y = 12
Từ đó tìm được x = 2, y = 2
b, Phương trình hoành độ giao điểm của d và (p):
x 2 - 2 x - m 2 + 2 m = 0 (1)
d cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung Oy <=> (1) có hai nghiệm trái dấu. Từ đó tìm được 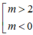
Kết luận 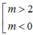

Phương trình hoành độ giao điểm:
\(x^2=2x-m+9\Leftrightarrow x^2-2x+m-9=0\) (1)
(d) cắt (P) tại 2 điểm nằm về 2 phía trục tung
\(\Leftrightarrow\) (1) có 2 nghiệm pb trái dấu
\(\Leftrightarrow ac< 0\Leftrightarrow m-9< 0\Rightarrow m< 9\)

b) (d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi
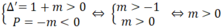
Khi đó 2 nghiệm của phương trình là:
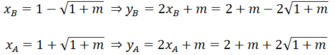
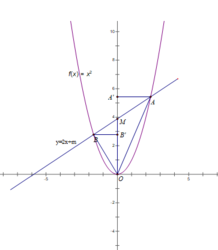
Kẻ BB' ⊥ OM ; AA' ⊥ OM
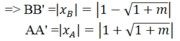
Ta có:
S A O M = 1/2 AA'.OM ; S B O M = 1/2 BB'.OM
Theo bài ra:
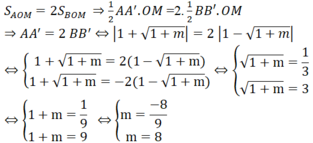
Do m > 0 nên m = 8
Vậy với m = 8 thì thỏa mãn điều kiện đề bài.

Xét phương trình hoành độ giao điểm
\(x^2=\left(m-1\right)x+m+4\Leftrightarrow x^2-\left(m-1\right)x-m-4=0\text{ }\left(\text{*}\right)\)
để d cắt P tại hai điểm phân biệt nằm ở hai phía của trục tung thì phương trình (*) có hai nghiệm trái dấu
khi đó điều kiện \(\Leftrightarrow-m-4< 0\Leftrightarrow m>-4\)
- Xét pt hoành độ gd....:
x2-(m-1)x-m-4=0 (1)
- để (P) cắt (d) tại 2 đm nằm về 2 phía của trục tung thì pt(1) có 2 nghiệm trái dấu nhau
- \(\left\{{}\begin{matrix}\Delta=\left(m-1\right)^2-4\left(-m-4\right)>0\\P=x_1x_2=-m-4< 0\Leftrightarrow m>-4\end{matrix}\right.\)
Vậy với m>-4 thì ....

a: 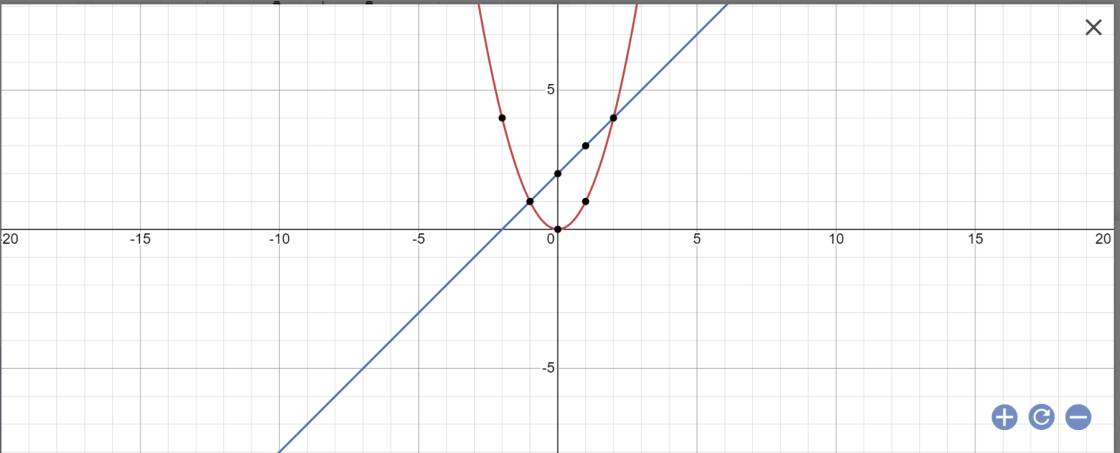
b: PTHĐGĐ là:
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
=>y=4 hoặc y=1
c: PTHĐGĐ là:
x^2-2x+m=0
Để (P) cắt (d1) tại hai điểm nằm về hai phía của trục tung thì m<0

đường thẳng \(d^'\)và \(d\)cắt nhau tại một điểm A trên trục tung nên điểm A có hoành độ \(x_a=0\)và tạo độ A thỏa mãn phương trình \(d^'\)nên :\(\Rightarrow y_a=-2.0+1=1\)\(\Rightarrow A\left(0;1\right)\)Mà do a là giao điểm của 2 đường \(d;d^'\)nên toạn độ A cũng thỏa mãn phương trình của \(d\): \(\Rightarrow1=-m^2+m+1\Leftrightarrow m^2-m=0\Leftrightarrow m\left(m-1\right)=0\Leftrightarrow m\orbr{\begin{cases}m=0\\m=1\end{cases}}\)
câu b :
Xét phương trình hoành độ gia điểm của P và d có :
\(x^2=2mx-m^2+m+1\Leftrightarrow x^2-2mx+m^2-m-1=0\)
để hai đồ thị cắt nhau tại 2 điểm phân biệt thì \(\Delta^'=m^2+m^2-m-1=2m^2-m-1>0\)
\(\left(m-1\right)\left(2m+1\right)>0\Leftrightarrow\orbr{\begin{cases}m< -\frac{1}{2}\\m>1\end{cases}}@\)
khi đó theo vieet có :\(\hept{\begin{cases}x_1+x_2=2m\\x_1x_2=-m^2+m+1\end{cases}}\)
\(\Rightarrow y_1+y_2+2\left(x_1+x_2\right)=22\)với \(y_1=x^2_1;y_2=x_2^2\)
\(\Rightarrow\left(\left(x_1+x_2\right)^2-2x_1.x_2\right)+\left(x_1+x_2\right)2=22\)thay vieet ta có :
\(\left(2m\right)^2-2\left(-m^2+m+1\right)+2.2m=22\)
\(\Leftrightarrow6m^2+2m-24=0\Leftrightarrow\orbr{\begin{cases}m=\frac{-1+\sqrt{144}}{6}\\m=\frac{-1-\sqrt{144}}{6}\end{cases}}\)thỏa mãn @
Kết luận nghiệm
tính denta sai rùi rùi bạn ơi
phải là 145 chứ ko phải 144

a: (d) có hệ số góc là m nên (d): y=mx+b
Thay x=-1 và y=-2 vào (d), ta được:
\(m\cdot\left(-1\right)+b=-2\)
=>b-m=-2
=>b=m-2
=>(d): y=mx+m-2
Phương trình hoành độ giao điểm là:
\(-x^2=mx+m-2\)
=>\(-x^2-mx-m+2=0\)
=>\(x^2+mx+m-2=0\)(1)
\(\text{Δ}=m^2-4\cdot1\cdot\left(m-2\right)\)
\(=m^2-4\left(m-2\right)\)
\(=m^2-4m+8=\left(m-2\right)^2+4>=4\forall m\)
=>(P) luôn cắt (d) tại hai điểm phân biệt
b: Để (P) cắt (d) tại hai điểm nằm về hai phía so với trục tung thì phương trình (1) phải có hai nghiệm phân biệt trái dấu
=>1(m-2)<0
=>m-2<0
=>m<2

1, Do hàm số trên cắt trục hoành tại điểm có hoành độ bằng 3 hay hàm số trên đi qua A(3;0)
<=> \(0=6+b\Leftrightarrow b=-6\)
2, Hoành độ giao điểm (P) ; (d) tm pt
\(x^2-\left(m-1\right)x-m+4=0\)
Để (P) cắt (d) tại 2 điểm pb nằm về 2 phía trục tung khi pt có 2 nghiệm trái dấu hay
\(x_1x_2=-m+4< 0\Leftrightarrow-m< -4\Leftrightarrow m>4\)
Chọn D