Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Phương pháp:
Bất phương trình m ≥ f x , x ∈ D có nghiệm khi và chỉ khi m ≥ M i n D f x .
Cách giải:
ĐKXĐ: 0 < x < 1
3 log x ≤ 2 log m x − x 2 − 1 − x 1 − x ⇔ m x − x 2 − 1 − x 1 − x ≥ x x
⇔ m ≥ x x + 1 − x 1 − x x − x 2 , x ∈ 0 ; 1
Để bất phương trình đã cho có nghiệm thực thì m ≥ M i n 0 ; 1 f x , f x = x x + 1 − x 1 − x x − x 2
Xét
f x = x x + 1 − x 1 − x x − x 2 = x + 1 − x 1 − x x − 1 x x − 1 , x ∈ 0 ; 1
Đặt t = x + 1 − x , t ∈ 1 ; 2
Khi đó,
f x = x + 1 − x 1 − x 1 − x x 1 − x = t 1 − t 2 − 1 2 t 2 − 1 2 = t 3 − t 2 t 2 − 1 = 3 t − t 3 t 2 − 1 = g t
g ' t = − t 4 − 3 t 2 − 1 2 < 0 , ∀ t ∈ 1 ; 2
⇒ g t min = g 2 = 3 2 − 2 2 2 − 1 = 2 ⇒ M i n 0 ; 1 f x = 2 ⇒ m ≥ 2
Mà
m ∈ − 9 ; 9 ⇒ m ∈ 2 ; 3 ; 4 ; ... ; 8 ⇒
Có 7 giá trị thỏa mãn.

Đáp án A
m + 3 m + 3 sin x 3 3 = s inx ⇔ m + 3 m + 3 sin x 3 = sin 3 x X 1 , … , X n ⇔ m + 3 sin x + 3 m + 3 sin x 3 = sin 3 x + 3 sin x ( 1 )
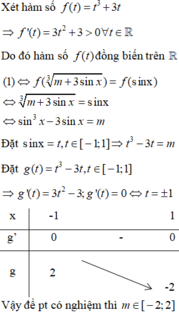

Đáp án A.
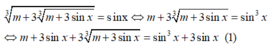
Xét hàm số f ( t ) = t 3 + 3 t ⇒ f ' ( t ) = 3 t 2 + 3 > 0 ∀ t ∈ R
Do đó hàm số f(t) đồng biến trên R
![]()
![]()
Đặt ![]()
Đặt
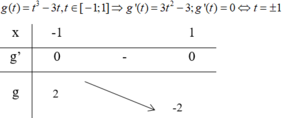
Vậy để pt có nghiệm thì m ∈ - 2 ; 2 .
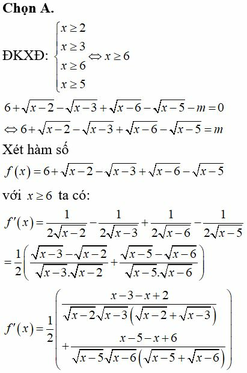

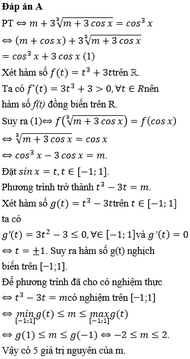
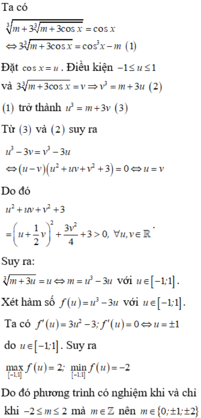





Đáp án C
Phương pháp:
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
Cách giải:
Xét hàm số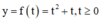
ta có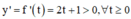
=> y = f(x) đồng biến trên khoảng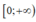
mà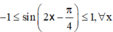
=> Để phương trình (2) có nghiệm thì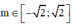
m ∈ Z => m ∈ {-1;0;1}
Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài