Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
*Phương trình m + 3 m + 3 sin x 3 3 = sin x ⇔ m + 3 m + 3 sin x 3 = sin 3 x
⇔ ( m + 3 sin x ) + 3 m + 3 sin x 3 = sin 3 x + 3 sin x ( 1 )
* Xét hàm số f ( t ) = t 3 + 3 t trên ℝ . Ta có f ' ( t ) = 3 t 2 + 3 > 0 ∀ t ∈ ℝ nên hàm số f(t) đồng biến trên ℝ .
Suy ra (1) f 3 + 3 sin x 3 f ( sin x ) ⇔ 3 + 3 sin x 3 = sin x
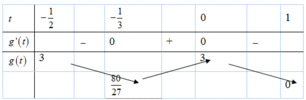
Đặt sin x = t, t ∈ [ - 1 ; 1 ] Phương trình trở thành t 3 - 3 t = m
* Xét hàm số g(t) trên t ∈ - 1 ; 1 Ta có g ' ( t ) = 3 t 2 - 3 ≤ 0 , ∀ t ∈ [ - 1 ; 1 ] và g ' ( t ) = 0 ⇔ t = ± 1 Suy ra hàm số g(t) nghịch biến trên [-1;1]
* Để phương trình có nghiệm đã cho có nghiệm thực ⇔ Phương trình t 3 - 3 t = m có nghiệm trên [-1;1]
m i n [ - 1 ; 1 ] g ( t ) ≤ m ≤ m a x [ - 1 ; 1 ] g ( t ) ⇔ g ( 1 ) ≤ m ≤ g ( - 1 ) ⇔ - 2 ≤ m ≤ 2
Vậy có 5 giá trị nguyên của m thỏa mãn là m ∈ - 2 ; - 1 ; 0 ; 1 ; 2

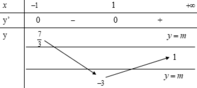
Chọn D.
Phương pháp: Biện luận nghiệm của phương trình theo m.
Cách giải: Ta có:


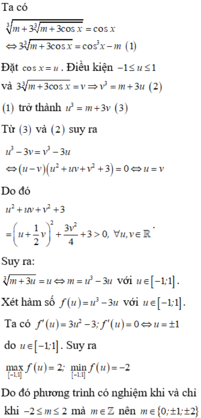
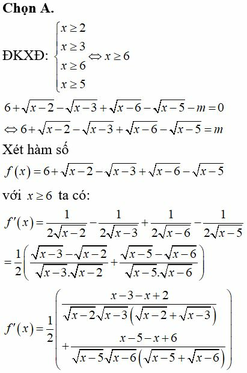






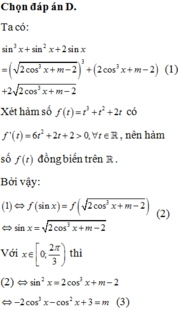


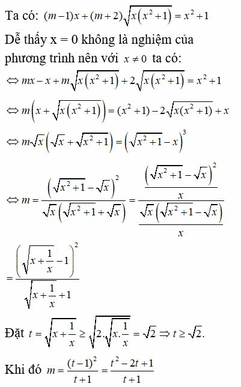



Đáp án A
Xét x ∈ - π ; π mà 1 + 2 sin x ≥ 0 1 + 2 cos x ≥ 0 suy ra x ∈ - π 6 ; 2 π 3
Ta có 1 + 2 cos x + 1 + 2 sin x = m 2 ⇔ m 2 8 = 1 + sin x + cos x + 1 + 2 sin x 1 + 2 cos x
Đặt t = sin x + cos x = 2 sin x + π 4 ⇒ t ∈ 3 - 1 2 ; 2 mà 2 sin x . cos x = t 2 - 1 .
Khi đó f t = 1 + t + 2 t 2 + 2 t - 1 , có f ' t = t + 2 t + 1 2 t 2 + 2 t - 1 > 0 , ∀ t ∈ 3 - 1 2 ; 2
Suy ra f(t) là hàm số đồng biến trên 3 - 1 2 ; 2 ⇒ m i n f t = f 2 = 2 + 2 2 m a x f t = f 3 - 1 2 = 1 + 3 2
Do đó, để f t = m 2 8 có nghiệm ⇔ 1 + 3 2 ≤ m 2 8 ≤ 2 + 2 2 ⇔ 2 1 + 3 ≤ m ≤ 4 1 + 2 .