Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ƯCLN(a,b)=6
=> a=6m ; b=6n ( ƯCLN(m,n)=1.)
Vì a+b=66
=> 6m+6n = 66
=> 6.(m+n) = 66
=> m+n =11
Vì ƯCLN(m,n)=1
=> (m;n) = ( 1;10) ; (2;9) ; (3;8) ; (4;7) ; ( 5;6 ) ; ( 6;5 ) ;( 7;4) ;( 8;3) ; (9;2) ;( 10;1)
=> (a;b) = ( 6;60) ; ( 12;54) ; (18;48) ;( 24;42) ;( 30;36) ;( 36;30) ;( 42;24) ; ( 48;18) ; ( 54;12 ) ;( 60;6)
Vì có 1 số chia hết cho 5
=> (a;b) = ( 6;60) ; ( 30;36) ; ( 36;30) ; (60;6)


a) Dễ thấy P = 102120 + 2120
= 102120 + 212.10
= 10(102119 + 212)
=> P \(⋮10\)
Lại có P = 102120 + 2120
= 10(102119 + 212)
= 10.(1000...00 + 212)
2119 số 0
= 10.1000...0212
2116 số 0
Tổng các chữ số của số S = 1000...0212 (2116 chữ số 0)
là 1 + 0 + 0 + 0 +.... + 0 + 2 + 1 + 2 (2116 hạng tử 0)
= 1 + 2 + 1 + 2 = 6 \(⋮3\)
=> S \(⋮3\Rightarrow P=10S⋮3\)
mà \(\left\{{}\begin{matrix}P⋮10\\P⋮3\\\left(10,3\right)=1\end{matrix}\right.\Rightarrow P⋮10.3\Rightarrow P⋮30\)
Gọi (a,b) = d \(\left(d\inℕ^∗;d\ne1\right)\)
=> \(\left\{{}\begin{matrix}a⋮d\\b⋮d\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2n+3⋮d\\5n+2⋮d\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}5.(2n+3)⋮d\\2.(5n+2)⋮d\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}10n+15⋮d\left(1\right)\\10n+4⋮d\left(2\right)\end{matrix}\right.\)
Lấy (1) trừ (2) ta được
(10n + 15) - (10n + 4) \(⋮d\)
<=> 11 \(⋮d\)
\(\Leftrightarrow d\in\left\{1;11\right\}\) mà d \(\ne1\)
<=> d = 11
Vậy (a;b) = 11
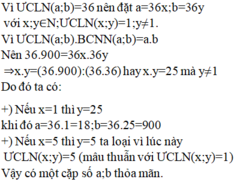
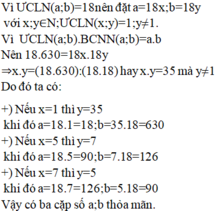
Gọi ước riêng lớn nhất của a;b lần lượt là m; n và (m; n) = 1
a = 6.m; b = 6.n
Theo bài ra ta có: 6.m + 6.n = 66
6.(m + n) = 66
m + n = 66 : 6
m + n = 11 vì (m; n ) = 1 nên ta có:
(m; n)=(1; 11); (2; 9); (3; 8); (4; 7);(5; 6);(6; 5);(7; 4); 8; 3); 9;2);(11;1)
Vì một trong hai số chia hết cho 5 nên (m; n) = (5; 6); (6;5)
Vậy có 2 cặp số (m; n) thì cũng có 2 cặp số (a; b) thỏa mãn đề bài.