Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số cách xếp ngẫu nhiên 12 học sinh thành hàng ngang là 12! cách.
Ta tìm số cách xếp thoả mãn:
Xếp hai bạn An và Bình cạnh nhau có 2! cách, gọi nhóm này là X;
Xếp 4 bạn lớp C còn lại cùng với X có 5! cách;
Lúc này có 4 vị trí (xen giữa các bạn lớp C còn lại và X) để xếp 3 bạn lớp B vào có A34A43cách;
Còn lại 3 vị trí để các bạn lớp A có thể xếp vào (1 vị trí xen giữa và ở hai đầu) có 3.3.3 cách.
Vậy có tất cả 2 ! 5 ! A 4 3 27 cách xếp thoả mãn.
Xác suất cần tính bằng 2 ! 5 ! A 4 3 27 12 ! = 1 3080
Chọn đáp án D.


Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
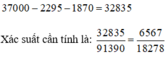
Chọn D

Gọi n là số học sinh nữ của lớp n ∈ N * , n ≤ 28 .
Số cách chọn 3 học sinh bất kì là cách. Suy ra số phần tử của không gian mẫu n Ω = C 30 3
Gọi A là biến cố “chọn được 2 nam và 1 nữ”. Ta có n A = C 30 - n 2 C n 1
Theo đề
P A = 12 29 ⇔ C 30 - n 2 C n 1 C 30 3 = 12 29 ⇔ n - 14 n 2 - 45 n + 240 = 0 ⇔ n = 14 n = 45 ± 1065 2
So với điều kiện, chọn n = 14
Vậy lớp đó có 14 học sinh nữ.
Đáp án A





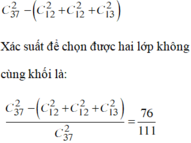
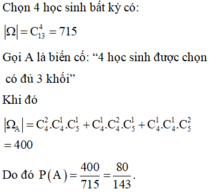
Chọn đáp án B.
Chọn ngẫu nhiên 5 học sinh trong 15 học sinh có C 15 5 = 3003 ⇒ n Ω = 3003
Gọi X là biến cố “tất cả các học sinh A đều được chọn”.
TH1. 2 học sinh lớp B, 0 học sinh lớp C ⇒ C 5 2 . C 7 0 = 10 cách.
TH2. 0 học sinh lớp B, 2 học sinh lớp C ⇒ C 5 0 . C 7 2 = 21 cách.
TH3. 1 học sinh lớp B, 1 học sinh lớp C ⇒ C 5 1 . C 7 1 = 35 cách.
Suy ra số phần tử của không gian mẫu là n(X)=10+21=35=66 Vậy P=2/91