K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
2
ND
Nguyễn Đức Trí
VIP
5 tháng 8 2023
\(\left(a-1\right)^2\ge0\Rightarrow a^2+1-2a\ge0\Rightarrow a^2+1\ge2a\left(1\right)\)
\(\left(2b-3\right)^2\ge0\Rightarrow4b^2+9-12b\ge0\Rightarrow4b^2+9\ge12b\left(2\right)\)
\(\left(c\sqrt[]{3}-\sqrt[]{3}\right)^2\ge0\Rightarrow3c^2+3-6c\ge0\Rightarrow3c^2+3\ge6c\left(3\right)\)
\(\left(1\right)+\left(2\right)+\left(3\right)\Rightarrow a^2+1+4b^2+9+3c^2+3\ge2a+12b+6c\)
\(\Rightarrow a^2+4b^2+3c^2+1+9+3\ge2a+12b+6c\)
\(\Rightarrow a^2+4b^2+3c^2+13\ge2a+12b+6c\)
\(\Rightarrow a^2+4b^2+3c^2\ge2a+12b+6c-13\)
mà \(2a+12b+6c-13>2a+12b+6c-14\)
\(\Rightarrow a^2+4b^2+3c^2>2a+12b+6c-14\)
\(\Rightarrow dpcm\)
26 tháng 6 2017
Bạn lạ ghê cho đề mà không nêu yêu cầu lấy gì mọi người giải được.
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 4 2019
\(\Leftrightarrow a^2-2a+1+4b^2-12b+9+3c^2-6c+3+1>0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(2b-3\right)^2+3\left(c-1\right)^2+1>0\) (luôn đúng)
\(\Rightarrow\) BĐT ban đầu đúng
NT
2
AH
Akai Haruma
Giáo viên
14 tháng 9
Lời giải:
$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$
$=(2a+b)^2-6(2a+b)+3b^2-6b+12$
$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$
$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$
Vậy $P_{\min}=0$
Giá trị này đạt tại $2a+b-3=b-1=0$
$\Rightarrow b=1; a=1$
AH
Akai Haruma
Giáo viên
14 tháng 9
Lời giải:
$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$
$=(2a+b)^2-6(2a+b)+3b^2-6b+12$
$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$
$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$
Vậy $P_{\min}=0$
Giá trị này đạt tại $2a+b-3=b-1=0$
$\Rightarrow b=1; a=1$
14 tháng 8 2023
1: 2a+2b=2(a+b)
2: 2a+4b+6c
=2*a+2*2b+2*3c
=2(a+2b+3c)
3: \(-7a-14ab-21b=-7\left(a+2ab+3b\right)\)
4: \(2ax-2ay+2a=2a\left(x-y+1\right)\)
5: \(=3a\cdot ax-3a\cdot2ay+3a\cdot4=3a\left(ax-2ay+4\right)\)
6: \(=2\cdot2ax-2\cdot ay-2\cdot1=2\cdot\left(2ax-ay-1\right)\)
7: =a^2-(2b)^2
=(a-2b)(a+2b)
8: =(5a)^2-1^2
=(5a-1)(5a+1)
9: =9(16a^2-9)
=9(4a-3)(4a+3)
10 tháng 5 2021
`a^2+b^2+c^2+d^2+1>=a+b+c+d`
`<=>4(a^2+b^2+c^2+d^2+1)>=4a+4b+4c+4d`
`<=>4a^2-4a+1+4b^2-4b+1+4c^2-4c+1+4d^2-4d+1>=0`
`<=>(2a-1)^2+(2b-1)^2+(2c-1)^2+(2d-1)^2>=0`(luôn đúng)
`=>a^2+b^2+c^2+d^2+1>=a+b+c+d`
Dấu "=" xảy ra khi `2a-1=2b-1=2c-1=2d-1=0<=>a=b=c=d=1/2`
HK
0
T
12 tháng 10 2019
Sửa đề: chứng minh:\(\frac{a^2}{\sqrt{12b^2+11bc+2c^2}}+\frac{b^2}{\sqrt{12c^2+11ca+2a^2}}+\frac{c^2}{\sqrt{12a^2+11ca+2b^2}}\ge\frac{3}{5}\)
Ta có: \(12b^2+11bc+2c^2=\frac{1}{4}\left(7b+3c\right)^2-\frac{1}{4}\left(b-c\right)^2\le\frac{1}{4}\left(7b+3c\right)^2\)
Do đó: \(\frac{a^2}{\sqrt{12b^2+11bc+2c^2}}\ge\frac{2a^2}{7b+3c}\).Tương tự hai BĐT còn lại rồi cộng theo vế thu được:
\(VT\ge\frac{2a^2}{7b+3c}+\frac{2b^2}{7c+3a}+\frac{2c^2}{7a+3b}\)
\(=2\left(\frac{a^2}{7b+3c}+\frac{b^2}{7c+3a}+\frac{c^2}{7a+3b}\right)\ge\frac{2\left(a+b+c\right)^2}{10\left(a+b+c\right)}=\frac{3}{5}\)(áp dụng BĐT Cauchy-Schwarz dạng Engel)
Ta có đpcm. Đẳng thức xảy ra khi a = b = c = 1
P/s: Is that true? Thấy đề nó là lạ nên sửa thôi chứ ko chắc rằng mình sửa đúng..
T
13 tháng 10 2019
@Cool Kid: Cách của mình"
Đầu tiên ta xét hiệu: \(12b^2+11bc+2c^2-x\left(b-c\right)^2\). Ta chọn x để biểu thức sau khi phân tích có dạng một số chính phương.
\(=\left(12-x\right)b^2+\left(11+2x\right)bc+\left(2-x\right)c^2\)
\(=\left(12-x\right)\left(b+\frac{\left(11+2x\right)c}{2\left(12-x\right)}\right)^2+\left(2-x\right)c^2-\frac{\left(11+2x\right)^2c^2}{4\left(12-x\right)}\)
\(=\left(12-x\right)\left(b+\frac{\left(11+2x\right)c}{2\left(12-x\right)}\right)^2+c^2\left[\left(2-x\right)-\frac{\left(11+2x\right)^2}{4\left(12-x\right)}\right]\)
Đến đây thì ý tưởng đã rõ, ta chọn x sao cho 12 - x > 0 và:
\(\left(2-x\right)-\frac{\left(11+2x\right)^2}{4\left(12-x\right)}=0\). Bấm máy tính ta suy ra \(x=-\frac{1}{4}\)
Từ đó có thể dễ dàng suy ra cách phân tích bên trên
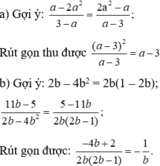
Ta có:
\(\left(a^2+4b^2+3c^2\right)-\left(20a+12b-6c-14\right)\)
\(=a^2+4b^2+3c^2-20a-12b-6c-14\)
\(=\left(a^2-2.a.10+100\right)+\left[\left(2b\right)^2-2.2b.3+9\right]+3\left(c^2+2c+1\right)-98\)
\(=\left(a-10\right)^2+\left(2b-3\right)^2+3\left(c+1\right)^2-98\ge-98\)
Vậy đề bài vô lý