TT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
Chứng minh rằng không tồn tại một tam giác có độ dài ba đường cao là 1; 3 ; 3 + 1 ( cùng đơn vị đo).
1
CM
21 tháng 2 2019
Giả sử tồn tại một tam giác có độ dài các đường cao là : h 1 = 1; h 2 = √3; h 3 = 1 + √3 (cùng đơn vị đo )
Gọi a 1 ; a 2 ; a 3 lần lượt là độ dài ba cạnh tương ứng với các đường cao h 1 ; h 2 ; h 3 .
Ta có: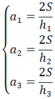 
a 1 ; a 2 ; a 3 lần lượt là 3 cạnh của tam giác nên:
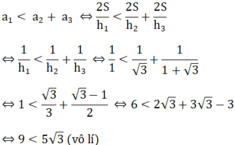
Vậy không tồn tại một tam giác có độ dài 3 đường cao lần lượt là 1; 3 1 + 3 (cùng đơn vị đo)
KN
0
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
AB=AC \(\Rightarrow\Delta ABC\) cân tại A
\(\Rightarrow AH\) đồng thời là phân giác và trung tuyến
\(\Rightarrow\left\{{}\begin{matrix}\widehat{BAH}=\dfrac{1}{2}\widehat{A}=60^0\\BH=\dfrac{1}{2}BC=6\end{matrix}\right.\)
Trong tam giác vuông ABH:
\(tan\widehat{BAH}=\dfrac{BH}{AH}\Rightarrow AH=\dfrac{BH}{tan\widehat{BAH}}=\dfrac{6}{tan60^0}=2\sqrt{3}\)
24 tháng 8 2020
Xét \(\Delta\)ABC có :
AH2 = BH.CH
AH2 = c'.b' (1)
Mà c'/b' = 1/3
=》3c' = b
Thay vào (1) ta có :
12 = c'.3c'
12 = 3c'2
c'2 = 4
=》 c' = 2 (cm)
=》b' = 3.2 = 6(cm)
=》 BC = 2 + 6 = 8 (cm)
Ta có : AB2 = BH.BC = 2.8 = 16
=》 AB = 4(cm)
Lại có AC2 = CH.BC = 6.8 = 48(cm)
=》 AC = 4\(\sqrt{ }\)3 (cm)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
\(\left(b^3+c^3\right)\left(1+1\right)\left(1+1\right)\ge\left(b+c\right)^3\)
\(\Rightarrow b^3+c^3\ge\dfrac{\left(b+c\right)^3}{4}\Rightarrow\dfrac{a}{\sqrt[3]{b^3+c^3}}\le\dfrac{a\sqrt[3]{4}}{b+c}\)
Tương tự và cộng lại:
\(VT\le\sqrt[3]{4}\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)< \sqrt[3]{4}\left(\dfrac{2a}{a+b+c}+\dfrac{2b}{a+b+c}+\dfrac{2c}{a+b+c}\right)=2\sqrt[3]{4}\)