K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
3
26 tháng 6 2015
Đặt ƯCLN\(\left(16n+5;24n+7\right)=d\)
=> 16n + 5 chia hết cho d và 24n + 7 chia hết cho d.
=> 3.(16n + 5) - 2.(24n + 7) chia hết cho d.
=> 48n + 15 - 38n + 14 chia hết cho d
=> 1 chia hết cho d
=> d = 1
suy ra điều phải chứng tỏ
VD
29 tháng 3 2017
Gọi d là UCLN(16n+5;24n+7)
=>16n+5 chia hết cho d và 24n+7 chia hết cho d
Vì:16n+5 chia hết cho d=>48n+15 chia hết cho d
24n+7 chia hết cho d=>48n+14 chia hết cho d
Ta có:(48n+15)-(48n+14) chia hết cho d
= 1 chia hết cho d
Vì d=1 nên \(\frac{18n+5}{24n+7}\)là phân số tối giản với mọi n.
Mình làm bài này rồi,đề thi HSG lớp 6 có bài này.
PT
1
PT
1
NV
1
7 tháng 2 2018
Gọi d là ƯCLN(16n+3,12n+2)
\(\Rightarrow\hept{\begin{cases}16n+3⋮d\\12n+2⋮d\end{cases}\Leftrightarrow\hept{\begin{cases}48n+9⋮d\\48n+8⋮d\end{cases}}}\)
\(\Rightarrow\left(48n+9\right)-\left(48n+8\right)⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
Vậy phân số 16n+3/12n+2 tối giản
25 tháng 4 2016
Đặt ƯCLN \(\left(16n+5;24n+7\right)\)
\(\Rightarrow\) 16 + 5 chia hết cho d và 24n + 7 chia hết cho d
\(\Rightarrow\) 3. ( 16n + 5 ) - 2 . ( 24n + 7 ) chia hết cho d
=> 48n + 15 - 38n + 14 chia hết cho d
=> 1 chia hết cho d
=> d = 1
Suy ra điều phải chứng tỏ
25 tháng 4 2016
Đặt \(ưcln\)\(\left(16n-5:24n+7\right)\)=\(d\)
=> 16n + 5 chia hết cho d và 24n + 7 chia hết cho d.
=> 3.(16n + 5) - 2.(24n + 7) chia hết cho d.
=> 48n + 15 - 38n + 14 chia hết cho d
=> 1 chia hết cho d
=> d = 1
suy ra điều phải chứng tỏ
NS
0
TH
1
12 tháng 2 2016
Gọi UCLN(16n+3,12n+2)=d
Ta có:16n+3 chia hết cho d =>3(16n+3) chia hết cho d =>48n+9 chia hết cho d
12n+2 chia hết cho d =>4(12n+2) chia hết cho d =>48n+8 chia hết cho d
=>(48n+9)-(48n+8) chia hết cho d
=>1 chia hết cho d
=>d=1
Vậy phân số 16n+3/12n+2 tối giản với mọi n là số tự nhiên
29 tháng 2 2016
a,Gọi d=(14n+3;21n+5)
=>14n+3 (2) và 21n+5 chia hết cho d
=>70n+15 và 63n+15 chi hết cho d => 7n chia hết cho d => 14n chia hết cho d (1)
Từ (1) và (2) => 3 chia hết cho d => d= 3 hoặc 1
+, Nếu d=3 => 21n+5 chia hết cho 3 => 5 chia hết cho 3 (vô lý) => d=1 =>đpcm
b, Gọi d=(16n+5;24n+7)
=> 16n+5 (4) và 24n+7 chia hết cho d
=>8n+2 chia hết cho d =>16n+4 chia hết cho d (3)
Từ (3) và (4) => d=1
15 tháng 3 2016
a) tìm tất cả các phân số có tử bằng 15 lớn hơn 3/7 và nhỏ hơn 5/8
b) tính tổng S = 4/2.5 + 4/5.8 + 4/8.11 + ... 4/65.68
c) chứng tỏ rằng 16n + 5 / 24n + 7 là phân số tối giản với mọi n thuộc z
Toán lớp 6
ai tích mình tích lại nh nha
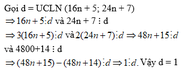
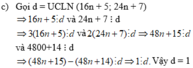
Gọi UCLN( 16n + 5; 24n + 7) là d.
Ta có:
16n + 5 chia hết cho d => 48n + 15 chia hết cho d ( 1 )
24n + 7 chia hết cho d => 48n + 14 chia hết cho d ( 2 )
Từ (1)(2) ta có: (48n + 15) - (48n +14) chia hết cho d => 1 chia hết cho d => d thuộc U(1) = { -1; 1}
Vậy 16n + 5; 24n + 7 là phân số tối giản.