NM
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 2 2021
Ta có:
A= 52014-52013+52012⋮105
A= 5^2011(5^3- 5^2)+5
A=5^2011(125- 25)+5
A= 5^2011. 105
=> A:105(đpcm)
3 tháng 2 2021
5^2014-5^2013+5^2012
=5^2012(5^2-5^1+1)
=5^2012.21 =5^2011.5.21
=5^2011.105
Vậy 5^2014-5^2013+5^2012 chia hết cho 105
chúc bạn học tốt
BF
1
12 tháng 8 2019
Ta có :
\(\frac{12}{-20}=\frac{3}{-5}\) ; \(\frac{12}{3}=-\frac{20}{-5}\)
\(-\frac{5}{-20}=\frac{3}{12}\); \(-\frac{5}{3}=-\frac{20}{12}\)
Chúc bạn học tốt !!!
19 tháng 8 2015
xét m tận cùng bằng 0 hoặc 5=>mn chia hết cho 5
xét m lẻ=>m4 có tận cùng bằng 1
=>24.m4+1 có tận cùng bằng 5
=>n có tận cùng bằng 5
=>mn chia hết cho 5
xét m chẵn=>m4 có tận cùng bằng 6
=>24.m4+1 có tận cùng bằng 5
=>n có tận cùng bằng 5
=>mn chia hết cho 5
từ các dữ liệu trên=>mn chia hết cho 5
=>đpcm
16 tháng 9 2023
a: \(4\cdot\dfrac{9}{9\cdot3}=\dfrac{4}{3};3\cdot\dfrac{12}{9\cdot3}=\dfrac{12}{9}=\dfrac{4}{3}\)
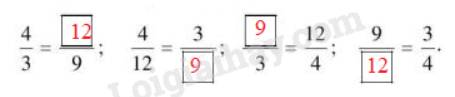
b: 4/3=12/9
4/12=3/9
9/3=12/4
9/12=3/4
4 tháng 1 2019
|x-2y-1|=10-5=5
x-2y-1=-5 hoac x-2y-1=5
x-2y=-4 hoac x-2y=6
............................................
............................................
D
1
14 tháng 3 2017
\(A=\left[-a^5.\left(-a^5\right)\right]^2+\left[-a^2.\left(-a^2\right)\right]^5=0\)O
=>\(\left(-a^{10}\right)^2+\left(-a^4\right)^5=a^{20}-a^{20}=0\)
\(B;\left(-1\right)^n.a^{a+k}=\left(-a\right)^n.a^k\)
\(=\left(-1\right)^n.a^n.a^k=\left(-1.a\right)^n.a^k\)
=\(\left(-a^n\right).a^k\)
Ta có : \(1+5+5^2+...+5^{2012}\)
Đặt : \(A=1+5+5^2+...+5^{2012}\)
\(\Rightarrow5A=5+5^2+5^3+...+5^{2013}\)
\(\Rightarrow5A-A=\left(5+5^2+...+5^{2013}\right)-\left(1+5+...+5^{2012}\right)\)
\(\Rightarrow4A=5^{2013}-1\)( Trừ vế theo vế )
\(\Rightarrow A=\frac{5^{2013}-1}{4}\left(đpcm\right)\)
Đặt \(A=1+5+5^2+...+5^{2012}\)
Ta có : \(5A=5+5^2+5^3+...+5^{2013}\)
\(\Rightarrow5A-A=\left(5+5^2+5^3+...+5^{2013}\right)-\left(1+5+5^2+...+5^{2012}\right)\)
\(\Rightarrow4A=5^{2013}-1\Rightarrow A=\frac{5^{2013}-1}{4}\RightarrowĐPCM\)