
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có
B = 8 5 − 2 11 = 2 3 5 − 2 11 = 2 15 − 2 11 = 2 11 .2 4 − 2 11 = 2 11 . 2 4 − 1 = 2 11 . 16 − 1 = 2 11 .15 v ì 15 ⋮ 15 ⇒ B = 15.2 11 ⋮ 15
Đáp án cần chọn là: C

b, B=202-192+182-172+...+22-12
=(202-192)+(182-172)+...+(22-12)
= (20-19)(20+19)+(18-17)(18+17)+..+(2-1)(2+1)
=39+35+...+3
=\(\xrightarrow[10sốhạng]{3+..+35+39}\)
=\(\frac{\left(39+3\right).10}{2}=210\)
Vậy B =210

ta có: \(28+211+2n=239+2n\)
Đặt \(239+2n=t^2\left(t\in N\right)\) \(\Rightarrow225+14+2n=t^2\)
\(\Rightarrow14+2n=t^2-15^2\Rightarrow2\left(n+7\right)=\left(t+15\right)\left(t-15\right)\)
\(\left(t+15\right)\left(t-15\right)⋮2\) mà 2 là số nguyên tố
nên \(\left(t+15\right)⋮2\) và \(\left(t-15\right)⋮2\)
\(\Rightarrow t=2k\pm15\left(k\in N\right)\)
\(\Rightarrow2\left(n+7\right)=\left(2k\pm15\right)^2-15^2\)
\(\Rightarrow2\left(n+7\right)=4k^2\pm60k+15^2-15^2\)
\(\Rightarrow2\left(n+7\right)=4k^2\pm60k\)
\(\Rightarrow2\left(n+7\right)=2\left(2k^2\pm30k\right)\)
\(\Rightarrow n+7=2k^2\pm30k\Rightarrow n=2k^2\pm30k-7\)
Vậy với \(n=2k^2\pm30k-7\)
thì \(28+211+2n\) là số chính phương


\(\dfrac{x-11}{89}\) +\(\dfrac{x-13}{87}+\dfrac{x-15}{85}+\dfrac{x-17}{83}\)=4
⇔\(\dfrac{x-11}{89}+\dfrac{x-13}{87}+\dfrac{x-15}{85}+\dfrac{x-17}{83}-4=0\)
⇔\(\dfrac{x-11}{89}-1+\dfrac{x-13}{87}-1+\dfrac{x-15}{85}-1+\dfrac{x-17}{83}-1=0\)
⇔\(\dfrac{x-100}{89}+\dfrac{x-100}{87}+\dfrac{x-100}{85}+\dfrac{x-100}{83}=0\)
⇔\(\left(x-100\right)\left(\dfrac{1}{89}+\dfrac{1}{87}+\dfrac{1}{85}+\dfrac{1}{83}\right)=0\)
\(Do\) \(\dfrac{1}{89}+\dfrac{1}{87}+\dfrac{1}{85}+\dfrac{1}{83}\)≠\(0\) nên x-100=0 nên x=100
KL........
⇔(\(\dfrac{x-11}{89}\)-1)+(\(\dfrac{x-13}{87}\)-1)+(\(\dfrac{x-15}{85}\)-1)+(\(\dfrac{x-17}{83}\)-1)=0
⇔\(\dfrac{x-100}{89}\)+\(\dfrac{x-100}{87}\)+\(\dfrac{x-100}{85}\)+\(\dfrac{x-100}{83}\)=0
⇔(x-100)(\(\dfrac{1}{89}\)+\(\dfrac{1}{87}\)+\(\dfrac{1}{85}\)+\(\dfrac{1}{83}\))=0 (1)
Do 1/89+1/87+1/85+1/83≠0 nên (1)⇔x-100=0 ⇔x=100
Vậy tập nghiệm của PT là S=\(\left\{100\right\}\)

\(\dfrac{x+14}{86}+\dfrac{x+15}{85}+\dfrac{x+16}{84}+\dfrac{x+17}{83}+\dfrac{x+116}{4}=0\)
\(\Leftrightarrow\left(\dfrac{x+14}{86}+1\right)+\left(\dfrac{x+15}{85}+1\right)+\left(\dfrac{x+16}{84}+1\right)+\left(\dfrac{x+17}{83}+1\right)+\left(\dfrac{x+116}{4}-1\right)=0\)
=>x+100=0
hay x=-100

ta có 0=\(\frac{x-11}{89}-1+\frac{x-13}{87}-1+\frac{x-15}{85}-1+\frac{x-17}{83}-1=0\)
0=\(\frac{x-11-89}{89}+\frac{x-13-87}{87}+\frac{x-15-85}{85}+\frac{x-17-83}{83}\)
0=\(\frac{x-100}{89}+\frac{x-100}{87}+\frac{x-100}{85}+\frac{x-100}{83}\)
0=(x-100)(\(\frac{1}{89}+\frac{1}{87}+\frac{1}{85}+\frac{1}{83}\))
vì \(\frac{1}{89}+\frac{1}{87}+\frac{1}{85}+\frac{1}{83}\)khác 0 suy ra x-100=0
x=100

\(\frac{x+14}{86}+\frac{x+15}{85}+\frac{x+16}{84}+\frac{x+17}{83}+\frac{x+116}{4}=0\)
\(\Leftrightarrow\frac{x+14}{86}+\frac{x+15}{85}+\frac{x+16}{84}+\frac{x+17}{83}+\frac{x+100}{4}+4=0\)
\(\Leftrightarrow\left(\frac{x+14}{86}+1\right)+\left(\frac{x+15}{85}+1\right)+\left(\frac{x+14}{86}+1\right)+\left(\frac{x+13}{87}+1\right)+\frac{x+100}{4}=0\)
\(\Leftrightarrow\frac{x+100}{86}+\frac{x+100}{85}+\frac{x+100}{84}+\frac{x+100}{83}+\frac{x+100}{4}=0\)
\(\Leftrightarrow\left(x+100\right)\left(\frac{1}{86}+\frac{1}{85}+\frac{1}{84}+\frac{1}{83}+\frac{1}{4}\right)=0\)
\(\Leftrightarrow x+100=0\left(vì\frac{1}{86}+\frac{1}{85}+\frac{1}{84}+\frac{1}{83}+\frac{1}{4}\ne0\right)\)
\(\Leftrightarrow x=-100\)
vậy.............................

a) (x-1)x(x+1)(x+2) = 24
<=> [(x-1)(x+2)][x(x+1) = 24
<=> (x^2+x-2)(x^2+x) = 24 (1)
Đặt t=x^2+x-1 = (x+1/2)^2 - 5/4 (*)
(1) trở thành (t-1)(t+1) = 24
<=> t^2 - 1 - 24 = 0
<=> t^2 - 25 = 0
<=> t^2 = 25
<=> t=5 hoặc t=-5
Mà t >= -5/4 ( từ *) => t = (x+1/2)^2-5/4 = 5
<=> (x+1/2)^2 = 25/4
Đến đây dễ r`
c) x^4 + 3x^3 + 4x^2 + 3x + 1 = 0
<=> x^4 + x^3 + 2x^3 + 2x^2 + 2x^2 + 2x + x + 1 = 0
<=> (x+1)(x^3 + 2x^2 + 2x + 1) = 0
<=> (x +1)(x^3 + x^2 + x^2 + x + x + 1) = 0
<=> (x+1)^2.(x^2+x+1) = 0
Mà x^2+x+1 = (x+1/2)^2 + 3/4 > 0
Nên x+1=0 <=> x=-1
Vậy ...

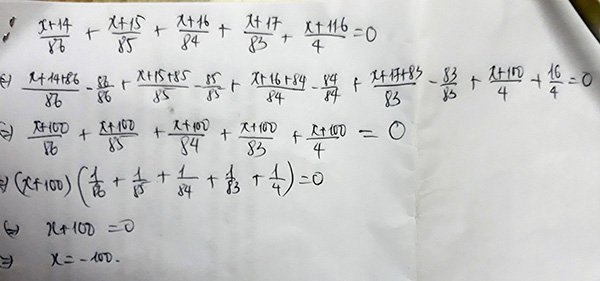
8^5+2^11
=2^15+2^11
=2^11(2^4+1)
=2^11*17 chia hết cho 17
Lời giải:
$8^5+2^{11}=(2^3)^5+2^{11}=2^{15}+2^{11}=2^{11}(2^4+1)=2^{11}.17\vdots 17$
Ta có đpcm.