
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) \(\left(\frac{2}{3}\right)^x=\left(\frac{4}{9}\right)^{50}\)
\(\Rightarrow\left(\frac{2}{3}\right)^x=\left(\frac{2^2}{3^2}\right)^{50}\)
\(\Rightarrow\left(\frac{2}{3}\right)^x=\left(\frac{2}{3}\right)^{100}\)
\(\Rightarrow x=100\)
Vậy x = 100
b) \(\left(\frac{2}{3}-x\right)^2=\frac{1}{36}\)
\(\Rightarrow\left(\frac{2}{3}-x\right)^2=\left(\frac{1}{6}\right)^2\)
\(\Rightarrow\frac{2}{3}-x=\frac{1}{6}\)
\(\Rightarrow x=\frac{2}{3}-\frac{1}{6}\)
\(\Rightarrow x=\frac{1}{2}\)
Vậy \(x=\frac{1}{2}\)
2)
Ta có:
\(74^{m+1}+74^m=74^m.74^1+74^m=74^m.\left(74+1\right)=74^m.75⋮25\)
( vì \(75⋮25\) )
\(\Rightarrowđpcm\)



Dễ thấy: \(A⋮9\)(tổng các chữ số của A là \(90\cdot8=720⋮9\))
\(B⋮9\)(tổng các chữ số của B là \(72\cdot1=72⋮9\))
\(\Rightarrow A+B⋮9\)(đpcm)

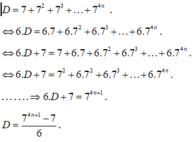
fix: \(l=\frac{1}{7^2}-\frac{1}{7^4}+...+\frac{1}{7^{4n-2}}-\frac{1}{7^{4n}}+...+\frac{1}{7^{98}}-\frac{1}{7^{100}}\)
\(49l=1-\frac{1}{7^2}+...+\frac{1}{7^{4n-4}}-\frac{1}{7^{4n-2}}+...+\frac{1}{7^{96}}-\frac{1}{7^{98}}\)
\(49l+l=\left(1-\frac{1}{7^2}+...+\frac{1}{7^{4n-4}}-\frac{1}{7^{4n-2}}+...+\frac{1}{7^{96}}-\frac{1}{7^{98}}\right)+\left(\frac{1}{7^2}-\frac{1}{7^4}+...+\frac{1}{7^{4n-2}}-\frac{1}{7^{4n}}+...+\frac{1}{7^{98}}-\frac{1}{7^{100}}\right)\)\(50l=1-\frac{1}{7^{100}}\Leftrightarrow l=\frac{1}{50}-\frac{1}{7^{100}.50}< \frac{1}{50}\left(đpcm\right)\)