Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Tại vị trí cân bằng vật đạt vận tốc có giá trị cực đại nên:
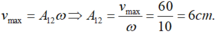
- Hai dao động cùng pha thì biên độ của dao động tổng hợp là:
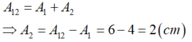

Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)

Phương trình tổng quát: \(x= A\cos(\omega t +\varphi)\)
Áp dụng công thức độc lập: \(A^2 = x^2 +\frac{v^2}{\omega ^2} \Rightarrow (\frac{x}{A})^2+(\frac{v}{\omega A})^2=1\)\(\Rightarrow\left\{ \begin{array}{} A^2 = 16\ \\ \omega^2 A^2 =640 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} A = 4\ \\ \omega =2\pi \end{array} \right.\)
t = 0\(\Rightarrow\left\{ \begin{array}{} x_0 = A/2\\ v_0 <0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = \frac{1}{2}=0,5\\ \sin \varphi >0 \end{array} \right. \Rightarrow \varphi = \frac{\pi}{3}\)
Phương trình dao động: \(x=4\cos(2\pi t +\frac{\pi}{3}) \ (cm)\)

Chọn đáp án C
x = x 1 + x 2 = 1. cos 10 t + π 4 ⇒ V max = ω . A = 10 c m / s .

Chọn đáp án C
Tại vị trí cân bằng vật đạt vận tốc có giá trị cực đại nên: v max = A 12 ω ⇒ A 12 = v max ω = 60 10 = 6 c m
Hai dao động cùng pha biên độ của dao động tổng hợp là A 12 = A 1 + A 2 ⇒ A 2 = A 12 - A 1 = 6 - 4 = 2 ( c m )

Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ


Đáp án B.
Lời giải chi tiết:
Tại vị trí cân bằng vật đạt vận tốc có giá trị cực đại nên:
Hai dao động cùng pha thì biên độ của dao động tổng hợp là