Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có :
ab=ba
=>a.10=b+b.10+a
=>a.11+b.11
=>11.(a+b) chia hết cho 11
duyệt mình đi mình nan nỉ đó
ta có:
ab+ba
=>a.10+b+b.10+a
=>a.11+b.11
=>11.(a+b) chịa hết cho 11

Gọi số đó là ab ( bất kì )
Ta có :
ab + ba
= 10a + b + 10b + a
= 11a + 11b
= 11 ( a + b ) chia hết cho 11 ( đpcm )
Vậy,........

c, Ta có ab+ba = 10a + 10b + a + b=11a + 11b
Vậy ab+ba chia hết cho 11

Gọi số A là bcd với b, c; d là chữ số
A = bcd và B = dcb
Nếu b = d -> A - B = 0 -> A - B chia hết cho 3
Nếu b > d x d
Thì bcd - dcb = 100 x b + 10 x c + d - 100 x d - 10 x c + b
= 99 x b - 99 x d = 99 x (b - d)
99 x (b - d) chia hết cho 3
A - B cũng chia hết cho
Nếu d > b cũng tương tư như trên
99 x (d - b) chia hết cho 3
Và A - B cũng chia hết cho 3
Kết luận : A - B chia hết cho 3
có chia được cho 3 nếu có điều kiện tổng các số chia hết cho 3
không nếu tổng các chữ số không chia hết được cho 3

Gọi số A là abc. Theo đề ta có :
\(A-B=\overline{abc}-\overline{cba}=\left(a-c\right)\cdot100+c-a=a\cdot100-c\cdot100+c-a=99\cdot a-99\cdot c\)
Mà 99 chia hết cho 9
Nên hiệu hai số A và B chia hết cho 9
Bài làm:
Đặt số tự nhiên bất kì đó là: \(A=\overline{abc}\) với \(\hept{\begin{cases}a>0\\b,c\ge0\end{cases}}\)
Khi đó \(B=\overline{cba}\)
Xét hiệu \(A-B=\overline{abc}-\overline{cba}\)
\(=100a+10b+c-100c-10b-a\)
\(=99a-99c=99\left(a-c\right)\)
Vì 99 chia hết cho 99 => 99(a-c) chia hết cho 99
=> A - B chia hết cho 99
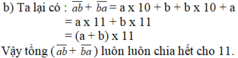
Ta có:
\(\overline{ab}\)=\(\overline{ba}\)
\(\Rightarrow a.10=b+b.10+a\)
\(\Rightarrow a.11+b.11\)
\(\Rightarrow11.\left(a+b\right)⋮11\)