
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=x^3\left(x+2\right)-x\left(x+2\right)\)
\(=\left(x+2\right)\cdot x\cdot\left(x+1\right)\left(x-1\right)\)
Vì đây là tích của bốn số nguyên liên tiếp
nên \(\left(x+2\right)\cdot x\cdot\left(x+1\right)\cdot\left(x-1\right)⋮24\)




Phần dư của phép chia đa thức x 4 + a x 2 + 1 chia hết cho x 2 + 2x + 1 là
R = (-4 – 2a)x – a – 2
Để phép chia trên là phép chia hết thì R = 0 ó (-4 – 2a)x – a – 2 = 0 với mọi x
ó - 2 a - 4 = 0 - a - 2 = 0 ó a = -2
Đáp án cần chọn là: A

Ta có
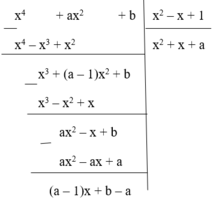
Phần dư của phép chia là R = (a – 1)x + b – A. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 1)x + b – a = 0, Ɐx
ó a - 1 = 0 b - a = 0 ó a = 1 b = 1 ó a = b
Đáp án cần chọn là: C

A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1

\(a,x^4-2x^3+6x^2+x+14\\ =\left(x^4-3x^3+7x^2\right)+\left(x^3-3x^2+7x\right)+\left(2x^2-6x+14\right)\\ =\left(x^2-3x+7\right)\left(x^2+x+2\right):\left(x^2-3x+7\right)=x^2+x+2\)
Ta có \(x^2+x+2=x^2+x+\dfrac{1}{4}+\dfrac{7}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}>0\)
Vậy ...
\(b,A=x^3+3xy+y^3\\ A=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\\ A=x^2-xy+y^2+3xy\\ A=x^2+2xy+y^2=\left(x+y\right)^2=1\)
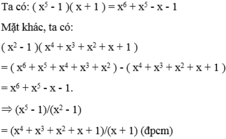
vì x^200 chia hết cho 4 , x^100 chia hết cho x^2 và 1 chia hết cho 1 nên x^200+x^100+1 chia hếtcho x^4+x^2+1
**** bn nhe
Đặt x2=ax2=a. Cần chứng minh: a^100+a^50⋮a2+a+1a100+a50⋮a2+a+1
Sử dụng tính chất quen thuộc: a3m+1+a3n+2=a(a3m−1)+a2(a3n−1)−(a2+a+1)⋮a2+a+1