K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HV
0
U
4
30 tháng 10 2015
\(A+A_1+B+B_1+C+C_1=3.180\)
Mà A+B+C=180=> \(A_1+B_1+C_1=360\)
SG
2
30 tháng 6 2017
Gọi A^1, B^1, C^1 là 3 góc trong của tam giác ABC. A^2, B^2,C^2 là 3 góc ngoài của tam giác ABC.
Ta có:
A^1 + A^2 = 1800
B^1 + B^2 = 1800
C^1 + C^2 = 1800
---------------------
Cộng vế theo vế được:
A^1 +B^1 +C^1 +A^2 +B^2 +C^2 = 3.1800
mà A^1 +B^1 +C^1 = 1800 (tổng 3 góc trong của tam giác)
=> A^2 +B^2 +C^2 = 3.1800 - 1800 = 2.1800 = 3600
NP
4
2 tháng 10 2016
Gọi A^1, B^1, C^1 là 3 góc trong của tam giác ABC. A^2, B^2,C^2 là 3 góc ngoài của tam giác ABC.
Ta có:
A^1 + A^2 = 180*
B^1 + B^2 = 180*
C^1 + C^2 = 180*
---------------------
Cộng vế theo vế được:
A^1 +B^1 +C^1 +A^2 +B^2 +C^2 = 3.180*
mà A^1 +B^1 +C^1 = 180* (tổng 3 góc trong của tam giác)
=> A^2 +B^2 +C^2 = 3.180* - 180* = 2.180* = 360*
2 tháng 10 2016
Ta có: góc ngoài của một tam giác bằng tổng 2 góc trong ko kề với nó
=> Tổng 3 góc ngoài của 1 tam giác bằng tổng 2 lần các góc trong ko kề với nó
Mà tổng 2 lần các góc trong ko kề với nó = 2 x (tổng 3 góc của 1 tam giác) = 2 x 1800 = 3600
Vậy tổng ba góc ngoài ở ba đỉnh của một tam giác bằng 3600
NY
0
GP
1
15 tháng 11 2015
Gọi A^1, B^1, C^1 là 3 góc trong của tam giác ABC. A^2, B^2,C^2 là 3 góc ngoài của tam giác ABC.
Ta có: A^1 + A^2 = 180* B^1 + B^2 = 180* C^1 + C^2 = 180*
---------------------
Cộng vế theo vế được: A^1 +B^1 +C^1 +A^2 +B^2 +C^2 = 3.180* mà A^1 +B^1 +C^1 = 180* (tổng 3 góc trong của tam giác)
=> A^2 +B^2 +C^2 = 3.180* - 180* = 2.180* = 360*
LF
0
M
1
3 tháng 11 2016
Gọi 3 góc ngoài ở 3 đỉnh của 1 tam giác lần lượt là A1;B1;C1 còn A2;B2;C2 là góc trong của tam giác.
Ta có:
A1 + A2 = 180o
B1 + B2 = 180o
C1 + C2 = 180o
=> A1+B1+C1+A2+B2+C2 = 360o
Mà A2 + B2 + C2 = 180o (tổng 3 góc trong của tam giác)
=> A1+B1+C1 = 360o-180o=180o.2 = 360o
29 tháng 8 2018
Chẳng những đối với tam giác mà đối với mọi đa giác lồi,tổng số đo các góc ngoài luôn luôn bằng 360 độ
Ở cuối chương tứ giác (lớp 8),em sẽ học công thức tổng quát tính tổng số đo các góc trong của n-giác lồi (n>=3) là: (n-2).180độ
Góc ngoài tại mỗi đỉnh là góc kề bù với góc trong tại đỉnh đó
Tại n- đỉnh ta có n-góc bẹt là tổng số đo của n-góc TRONG và NGOÀI của n-giác lồi
Vậy tổng số đo n- góc ngoài của n-giác lồi là
n.180độ - (n-2).180độ=2.180độ=360độ
-----------------
PT
1
CM
26 tháng 7 2018
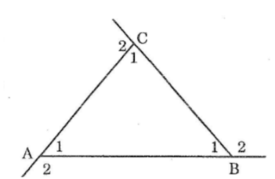
Ta có: ∠(A1 ) +∠(A2 ) =180o(hai góc kề bù)
∠(B1 ) +∠(B2 ) =180o(hai góc kề bù)
∠(C1 ) +∠(C2 )=180o(hai góc kề bù)
Suy ra: ∠(A1 ) +∠(A2 ) +∠(B1) +∠(B2 ) +∠(C1 ) +∠(C2 ) = 180º + 180º + 180º =540o
⇒∠(A2 ) + ∠( B2 ) +∠(C2 ) =540o-(∠(A1 ) +∠(B1 ) +∠(C1 ) ) (1)
Trong ΔABC, ta có:
∠(A1 ) +∠(B1 ) +∠(C1 ) =180o (tổng ba góc trong tam giác) (2)
Từ (1) và (2) suy ra: ∠(A2 ) +∠(B2 ) +∠(C2 ) =540o-180o=360o
Ta có hình vẽ :
=> \(\left\{{}\begin{matrix}\widehat{x}=\widehat{A}+\widehat{B}\\\widehat{y}=\widehat{B}+\widehat{C}\\\widehat{z}=\widehat{C}+\widehat{A}\end{matrix}\right.\)
=> \(\widehat{x}+\widehat{y}+\widehat{z}=\widehat{A}+\widehat{B}+\widehat{B}+\widehat{C}+\widehat{C}+\widehat{A}\)
= \(\left(\widehat{A}+\widehat{A}\right)+\left(\widehat{B}+\widehat{B}\right)+\left(\widehat{C}+\widehat{C}\right)\)
= \(2\widehat{A}+2\widehat{B}+2\widehat{C}\)
= \(2\left(\widehat{A}+\widehat{B}+\widehat{C}\right)\)
Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}\) = 180o ( Định lý tổng 3 góc của 1 tam giác )
\(\Rightarrow2\left(\widehat{A}+\widehat{B}+\widehat{C}\right)\) = 2.180o = 360o
=> đpcm