Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

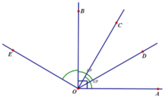
a) Vì tia OD nằm trong A O B ^ nên tia OD nằm giữa hai tia OA và OB do đó
A O D ^ + B O D ^ = A O B ^
Suy ra: A O D ^ = A O B ^ − B O D ^ = 90 0 − 60 0 = 30 0
Tương tự ta cũng có C O B ^ = 30 0 , D O C ^ = 30 0 .
b) Vì là tia phân giác của D O E ^ nên D O B ^ = B O E ^ = 60 0 .
Vì OB nằm giữa hai tia OC và OE và C O B ^ = 30 0 nên ta có
E O C ^ = E O B ^ + B O C ^ = 60 0 + 30 0 = 90 0
Vậy O C ⊥ O E

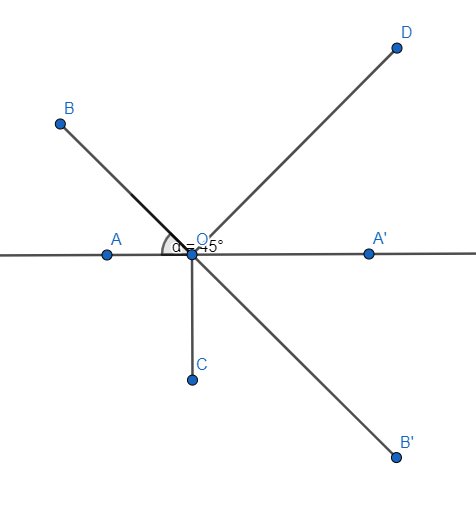
a) Vì OB' là tia phân giác của \(\widehat{A'OC}\) nên \(\widehat{A'OB'}=\dfrac{\widehat{A'OC}}{2}=\dfrac{90^o}{2}=45^o\). Suy ra \(\widehat{AOB}=\widehat{A'OB'}\left(=45^o\right)\). Lại có \(\widehat{AOB}+\widehat{BOA'}=\widehat{AOA'}=180^o\) nên \(\widehat{BOB'}=\widehat{A'OB'}+\widehat{BOA'}=180^o\) hay B, O, B' thẳng hàng. Suy ra \(\widehat{AOB}\) và \(\widehat{A'OB'}\) là 2 góc đối đỉnh.
b) Trên cùng 1 nửa mặt phẳng bờ là đường thẳng AA', ta thấy tia OB nằm giữa 2 tia OA và OD, tia OD lại nằm giữa 2 tia OB và OA', do đó \(\widehat{AOB}+\widehat{BOD}+\widehat{DOA'}=\widehat{AOA'}\) \(\Leftrightarrow45^o+90^o+\widehat{A'OD}=180^o\) \(\Leftrightarrow\widehat{A'OD}=45^o\)

a) Vì OB' là tia p/g của góc A'OC nên góc A'OB' = A'OC /2 = 90o/ 2 = 45o
Vì tia OB' nằm giữa hai tia OA và OA' nên góc A'OB' + B' OA = A'OA
=> 45o + B'OA = 180o
=> B'OA = 180o - 45o = 135o
=> Góc B'OA + AOB = 135o + 45o = 180o Mà tia OA nằm giữa 2 tia OB và OB' ( Vì tia OB và OB' nằm ở nửa mp khác nhau bờ là AA')
=> góc BOB' = 180o => tia OB và OB' đối nhau
ta có góc AOB = A'OB' (= 45o) Mà tia OA và OA' đối nhau ; tia OB và OB' đối nhau
=> 2 góc AOB và A'OB' đối nhau
b) Tia OD nằm giữa 2 tia OB và OB' => góc B'OD + DOB = BOB"
=> B'OD + 900 = 180o
=> B'OD = 90o
Lại có tia OA' nằm giữa 2 tia OD và OB'
=> góc A'OB' + A'OD = B'OD
=> 45o + A'OD = 90o => góc A'OD = 45o

a) Ta có :
OC vuông góc với OA = 90°
Mà OB' là phân giác A'OC
=> A'OB' = 90/2 = 45°
Mà OA là tia đối OA' (gt)
=> AOB = A'OB' = 45°
b) Vì B'OD = 90°
Mà A'OB' = 45°(cmt)
=> A'OD = 45°
=> A'OD = A'OB' = 45°
=> OA' là phân giác B'OD
Cho tam giác ABC, tia phân giác trong AD , M là điểm bất kì thuộc đường thẳng BC. Qua M vẽ đường thẳng song song với AD cắt AB,AC lần lượt tại P,Q. Chứng minh rằng tam giác APQ có hai góc bằng nhau

+) Tia OB nằm giữa 2 tia OA và OA' => góc AOB + BOA' = AOA' => 45 o + BOA' = 180 o => góc BOA' = 180 o - 45 o = 135 o
+) Tia OC nằm giữa 2 tia OA và OA' => góc A'OC + COA = AOA' => góc A'OC = 180 o - 90 o = 90 o
+) Tia OB' là tia p/g của góc A'OC => góc A'OB' = góc A'OC/2 = 45 o
và tia OB' nằm giữa 2 tia OA' và OC => tia OB' và OC nằm cùng nửa mp bờ chứa tia OA'
mà OC và OB nằm hai nửa mp bờ chứa tia OA'
=> tia OB' và OB nằm 2 nửa mp bờ chứa tia OA' => tia OA' nằm giữa 2 tia OB và OB'
=> góc BOA' + A'OB' = BOB'
=> 135 o + 45 o = BOB' => góc BOB' = 180 o => tia OB và OB' đối nhau mà 2 tia OA và OA' đối nhau
=> góc AOB và A'OB' đối đỉnh
a: Ta có: \(\widehat{A'OC}+\widehat{AOC}=180^0\)(kề bù)
=>\(\widehat{AOC}+90^0=180^0\)
=>\(\widehat{AOC}=90^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\widehat{AOB}< \widehat{AOC}\)
nên tia OB nằm giữa hai tia OA và OC
=>\(\widehat{AOB}+\widehat{BOC}=\widehat{AOC}\)
=>\(\widehat{BOC}=90^0-45^0=45^0\)
Ta có: \(\widehat{AOB}=\widehat{BOC}\)
mà tia OB nằm giữa hai tia OA và OC
nên OB là phân giác của góc AOC
b: Ta có: \(\widehat{COB}+\widehat{COE}=180^0\)(hai góc kề bù)
=>\(\widehat{COE}+45^0=180^0\)
=>\(\widehat{COE}=135^0\)