Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
Đặt \(a = BC,b = AC,c = AB\)
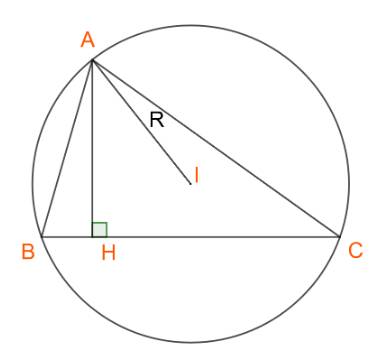
Ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b} \Rightarrow {h_a} = b.\sin C\)
Theo định lí sin, ta có: \(\frac{b}{{\sin B}} = 2R \Rightarrow b = 2R.\sin B\)
\( \Rightarrow {h_a} = 2R.\sin B.\sin C\)

Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2.AC.AB.\cos A\)
\( \Rightarrow \cos A = \frac{{A{C^2} + A{B^2} - B{C^2}}}{{2.AB.AC}} = \frac{{{7^2} + {6^2} - {8^2}}}{{2.7.6}} = \frac{1}{4}\)
Lại có: \({\sin ^2}A + {\cos ^2}A = 1 \Rightarrow \sin A = \sqrt {1 - {{\cos }^2}A} \)(do \({0^o} < A \le {90^o}\))
\( \Rightarrow \sin A = \sqrt {1 - {{\left( {\frac{1}{4}} \right)}^2}} = \frac{{\sqrt {15} }}{4}\)
Áp dụng định lí sin trong tam giác ABC ta có:\(\frac{{BC}}{{\sin A}} = 2R\)
\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{8}{{2.\frac{{\sqrt {15} }}{4}}} = \frac{{16\sqrt {15} }}{{15}}.\)
Vậy \(\cos A = \frac{1}{4};\)\(\sin A = \frac{{\sqrt {15} }}{4};\)\(R = \frac{{16\sqrt {15} }}{{15}}.\)

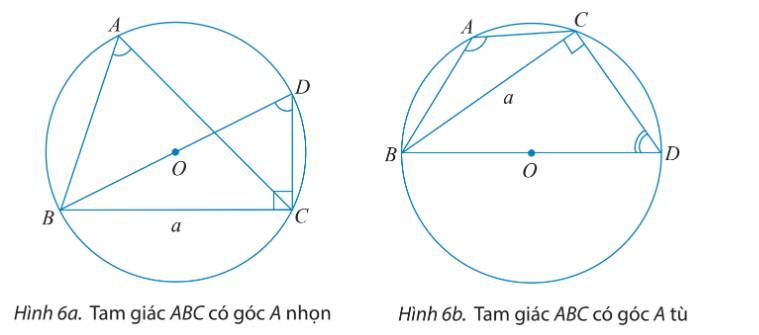
a) Tam giác BDC vuông tại C nên \(\sin \widehat {BDC} = \frac{{BC}}{{BD}} = \frac{a}{{2R}}.\)
b)
TH1: Tam giác ABC có góc A nhọn
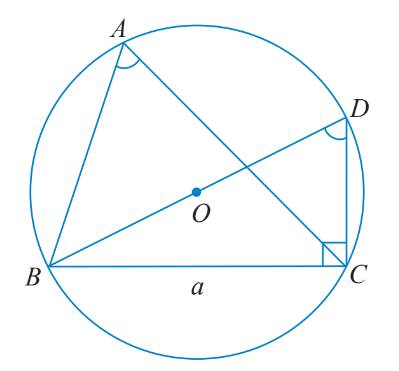
\(\widehat {BAC} = \widehat {BDC}\) do cùng chắn cung nhỏ BC.
\( \Rightarrow \sin \widehat {BAC} = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
TH2: Tam giác ABC có góc A tù
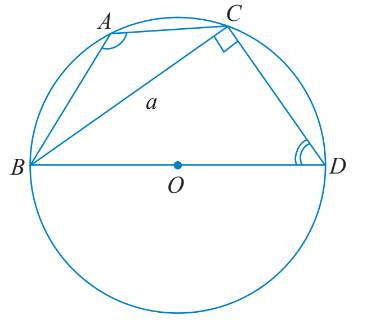
\(\widehat {BAC} + \widehat {BDC} = {180^o}\) do ABDC là tứ giác nội tiếp (O).
\( \Rightarrow \sin \widehat {BAC} = \sin ({180^o} - \widehat {BAC}) = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
Vậy với góc A nhọn hay tù ta đều có \(2R = \frac{a}{{\sin A}}.\)
b) Nếu tam giác ABC vuông tại A thì BC là đường kính của (O).
Khi đó ta có: \(\sin A = \sin {90^o} = 1\) và \(a = BC = 2R\)
Do đó ta vẫn có công thức: \(2R = \frac{a}{{\sin A}}.\)
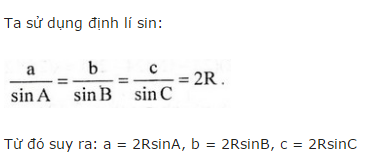

Ta có:
\(r^2+p^2+4Rr=\left(\dfrac{S}{p}\right)^2+p^2+\dfrac{abc}{S}.\dfrac{S}{p}\)
\(=\dfrac{\left(p-a\right)\left(p-b\right)\left(p-c\right)}{p}+p^2+\dfrac{abc}{p}\)
\(=\dfrac{p^3+\left(ab+bc+ac\right)p-p^2\left(a+b+c\right)-abc+p^3+abc}{p}\)
\(=ab+bc+ca\)
Do đó:
\(\dfrac{ab+bc+ca}{4R^2}=\dfrac{r^2+p^2+4Rr}{4R^2}\)
\(\Leftrightarrow sinAsinB+sinBsinC+sinCsinA=\dfrac{r^2+p^2+4Rr}{4R^2}\)\(\left(đpcm\right)\)
bạn giải thích chi tiết đoạn này hộ mình được ko ạ
p^3+(ab+bc+ac)p−p^2(a+b+c)−abc+p^3+abc/p
=ab+bc+ca