Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tam giác BDC vuông tại C nên \(\sin \widehat {BDC} = \frac{{BC}}{{BD}} = \frac{a}{{2R}}.\)
b)
TH1: Tam giác ABC có góc A nhọn
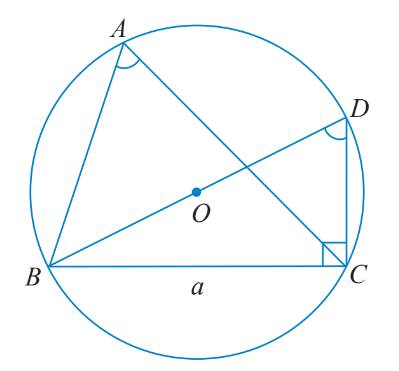
\(\widehat {BAC} = \widehat {BDC}\) do cùng chắn cung nhỏ BC.
\( \Rightarrow \sin \widehat {BAC} = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
TH2: Tam giác ABC có góc A tù
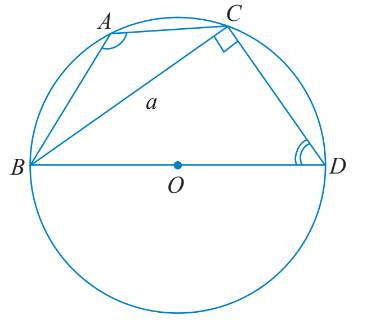
\(\widehat {BAC} + \widehat {BDC} = {180^o}\) do ABDC là tứ giác nội tiếp (O).
\( \Rightarrow \sin \widehat {BAC} = \sin ({180^o} - \widehat {BAC}) = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
Vậy với góc A nhọn hay tù ta đều có \(2R = \frac{a}{{\sin A}}.\)
b) Nếu tam giác ABC vuông tại A thì BC là đường kính của (O).
Khi đó ta có: \(\sin A = \sin {90^o} = 1\) và \(a = BC = 2R\)
Do đó ta vẫn có công thức: \(2R = \frac{a}{{\sin A}}.\)

Áp dụng định lí Cosin, ta có B C 2 = A B 2 + A C 2 − 2 A B . A C . cos B A C ^
= 3 2 + 6 2 − 2.3.6. c o s 60 0 = 27 ⇔ B C 2 = 27 ⇔ B C 2 + A B 2 = A C 2 .
Suy ra tam giác ABC vuông tại B, do đó bán kính R = A C 2 = 3.
Chọn A.

Chọn B.
Áp dụng định lí Cosin, ta có
BC2 = AB2 + AC2 - 2AB.AC.cosA
= 32 + 62-2.3.6.cos600 = 27
Ta thấy: BC2 + AB2 = AC2
Suy ra tam giác ABC vuông tại B
do đó bán kính R = AC : 2 = 3.

Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = 7,{5^2} + 3,{5^2} - 2.7,5.3,5.\cos {135^o}\\ \Leftrightarrow B{C^2} \approx 105,6\\ \Leftrightarrow BC \approx 10,3\end{array}\)
Áp dụng định lí sin trong tam giác ABC ta có: \(\frac{{BC}}{{\sin A}} = 2R\)
\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{{10,3}}{{2.\sin {{135}^o}}} \approx 7,3\)

Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2.AC.AB.\cos A\)
\( \Rightarrow \cos A = \frac{{A{C^2} + A{B^2} - B{C^2}}}{{2.AB.AC}} = \frac{{{7^2} + {6^2} - {8^2}}}{{2.7.6}} = \frac{1}{4}\)
Lại có: \({\sin ^2}A + {\cos ^2}A = 1 \Rightarrow \sin A = \sqrt {1 - {{\cos }^2}A} \)(do \({0^o} < A \le {90^o}\))
\( \Rightarrow \sin A = \sqrt {1 - {{\left( {\frac{1}{4}} \right)}^2}} = \frac{{\sqrt {15} }}{4}\)
Áp dụng định lí sin trong tam giác ABC ta có:\(\frac{{BC}}{{\sin A}} = 2R\)
\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{8}{{2.\frac{{\sqrt {15} }}{4}}} = \frac{{16\sqrt {15} }}{{15}}.\)
Vậy \(\cos A = \frac{1}{4};\)\(\sin A = \frac{{\sqrt {15} }}{4};\)\(R = \frac{{16\sqrt {15} }}{{15}}.\)