Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
Giả sử số thỏa mãn đề bài có dạng a 1 a 2 . . . a 2018
Do a 1 ≠ 0 nên a 1 = 1 .Và a 1 a 2 . . . a 2018 chia hết cho 5 nên a 2018 = 0
Lại có tổng a 1 + a 2 + . . . + a 2018 là một số chẵn, nên trong các chữ số a 2 , a 3 , . . . , a 2017 sẽ có một số lẻ chữ số 1.
Nếu trong các chữ số a 2 , a 3 , . . . , a 2017 có 1 chữ số 1 thì có tất cả C 2016 1 số thỏa mãn.
Nếu trong các chữ số a 2 , a 3 , . . . , a 2017 có 3 chữ số 1 thì có tất cả C 2016 3 số thỏa mãn.
Nếu trong các chữ số a 2 , a 3 , . . . , a 2017 có 5 chữ số 1 thì có tất cả C 2016 5 số thỏa mãn.
….
Tương tự, nếu trong các chữ số a 2 , a 3 , . . . , a 2017 có 2015 chữ số 1 thì có C 2016 2015 số thỏa mãn.
Vậy có tất cả C 2016 1 + C 2016 3 + . . . + C 2016 2015 số thỏa mãn yêu cầu đề bài đã cho.
Thay x = 1 và x = -1 vào hai khai triển trên ta có:
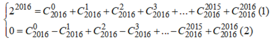
Trừ theo vế của (1) cho (2) ta được:
![]()
![]()

Chọn đáp án A.
Có 4 7 số tự nhiên có 7 chữ số được lập từ 4 số đã cho.
Số cần lập có 3 chữ số chẵn và 4 chữ số lẻ nên nó có dạng L C L C L C L ¯
Sắp xếp các số 1,3,1,3 vào 4 vị trí lẻ có 4 ! 2 ! . 2 ! = 6 cách.
Sắp xếp các số 2,2,4 vào 3 vị trí còn lại có: 3!/2!=3 cách.
Theo quy tắc nhân cầm tìm là: 6 . 3 4 7 = 9 8182

4a.
Số tự nhiên là A, ta có:
A = 7m + 5
A = 13n + 4
=>
A + 9 = 7m + 14 = 7(m + 2)
A + 9 = 13n + 13 = 13(n+1)
vậy A + 9 là bội số chung của 7 và 13
=> A + 9 = k.7.13 = 91k
<=> A = 91k - 9 = 91(k-1) + 82
vậy A chia cho 91 dư 82
4b.
Giả sử p là 1 số nguyên tố >3, do p không chia hết cho 3 nên p có dạng 3k + 1 hoặc 3k + 2
Vì p +4 là số nguyên tố nên p không thể có dạng 3k + 2
Vậy p có dạng 3k +1.
=> p + 8 = 3k + 9 chia hết cho 3 nên nó là hợp số.

bài 2 ta giải cách khác
Theo đề bài , ta gọi a là số An nghĩ . Ta có :
a-8 chia hết cho 7 => a-1 chia hết cho 7 (1)
a-9 chia hết cho 8 => a-1 chia hết cho 8 (2)
a-10 chia hết cho 9=> a-1 chia hết cho 9(3)
Từ (1) ; (2); (3), ta có a-1 là BC(7 ; 8 ; 9)
Ta có :
7 = 1 x 7
8 = 23
9 = 32
=> BCNN(7 ; 8 ; 9)= 7 x 23 x 32= 504
=> a-1thuộc B(504)= { 0;504;1008;.........................}
=> a thuộc { 1;505;1009;....................................}
Mà a là số có 3 chữ số
=> a = 505
Kết luận : Vậy số mà bạn An nghĩ ra là số 505
gọi số phải tìm là n
ta có:
n = 7.k + 8 = 7(k+1) +1
n = 8.m + 9= 8(m+1) +1
n = 9.p +10 = 9(p+1) +1
* từ đó thấy rằng số n là bội số chung của 7,8,9 +1
vậy số nhỏ nhất n= 7.8.9 +1 = 505
vì n là số có 3 chữ số n=505 là duy nhất
* thử lại:
(505-8)/7= 71
(505-9)/8= 62
(505-10)/9=55

Câu 1 : Việc gõ ký hiệu như bạn đề cập ; mình cũng không biết phải làm sao nên cứ dùng xyz vậy thôi.
Ta có:
xyz = 100x +10y +z = 111x -11x +10y +z = 37.3x -(11x-10y-z) chia hết cho 37
=> (11x-10y-z) chia hết cho 37
Lại có:
xyz -yzx = 100x +10y +z -100y -10z -x = 99x -90y -9z = 9.(11x-10y-z) chia hết cho 37
Vậy yzx cũng phải chia hết cho 37
Có thể phát biểu hay hơn là CMR: Khi hoán vị các chữ số của 1 số có 3 chữ số chia hết cho 37 thì được số mới cũng chia hết cho 37.

Vì có 11 tổng mà chỉ có thể có 10 chữ số tận cùng đều là các số từ 0 , 1 ,2, …., 9 nên luôn tìm được hai tổng có chữ số tận cùng giống nhau nên hiệu của chúng là một số nguyên có tận cùng là 0 và là số chia hết cho 10.
