Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử \(n+1=a^2\) ; \(2n+1=b^2\) \(\left(a,b\in N^{\text{*}}\right)\)
Ta có b là số lẻ \(\Leftrightarrow b=2m+1\Rightarrow b^2=4m\left(m+1\right)+1\Rightarrow n=2m\left(m+1\right)\)
=> n chẵn => n + 1 lẻ => a lẻ => a = 2k+1 => \(n+1=\left(2k+1\right)^2=4k\left(k+1\right)+1\Rightarrow n=4k\left(k+1\right)⋮8\)
Vậy n chia hết cho 8
Ta có : \(a^2+b^2=3n+2\equiv2\)(mod 3)
Mặt khác : \(b^2\)chia 3 dư 0 hoặc 1 , \(a^2\)chia 3 dư 0 hoặc 1
=> Để \(a^2+b^2\equiv2\)(mod 3) thì \(a^2\equiv1\)(mod 3) và \(b^2\equiv1\)(mod 3)
\(\Rightarrow b^2-a^2\)chia hết cho 3
Ta có : n = (2n + 1) - (n + 1) = \(b^2-a^2\)chia hết cho 3
Như vậy \(n⋮3,n⋮8\) mà (3,8) = 1
=> \(n⋮24\)

a là số tự nhiên > 0. giả sử có m,n > 0 ∈ Z để:
2a + 1 = n^2 (1)
3a +1 = m^2 (2)
từ (1) => n lẻ, đặt: n = 2k+1, ta được:
2a + 1 = 4k^2 + 4k + 1 = 4k(k+1) + 1
=> a = 2k(k+1)
vậy a chẵn .
a chẳn => (3a +1) là số lẻ và từ (2) => m lẻ, đặt m = 2p + 1
(1) + (2) được:
5a + 2 = 4k(k+1) + 1 + 4p(p+1) + 1
=> 5a = 4k(k+1) + 4p(p+1)
mà 4k(k+1) và 4p(p+1) đều chia hết cho 8 => 5a chia hết cho 8 => a chia hết cho 8
ta cần chứng minh a chia hết cho 5:
chú ý: số chính phương chỉ có các chữ số tận cùng là; 0,1,4,5,6,9
xét các trường hợp:
a = 5q + 1=> n^2 = 2a+1 = 10q + 3 có chữ số tận cùng là 3 (vô lý)
a =5q +2 => m^2 = 3a+1= 15q + 7 có chữ số tận cùng là 7 (vô lý)
(vì a chẵn => q chẵn 15q tận cùng là 0 => 15q + 7 tận cùng là 7)
a = 5q +3 => n^2 = 2a +1 = 10a + 7 có chữ số tận cùng là 7 (vô lý)
a = 5q + 4 => m^2 = 3a + 1 = 15q + 13 có chữ số tận cùng là 3 (vô lý)
=> a chia hết cho 5
5,8 nguyên tố cùng nhau => a chia hết cho 5.8 = 40
hay : a là bội số của 40

2n+1=a^2 (1), 3n+1=b^2 (2)
Từ (1) suy ra a lẻ, đặt a=2k+1 suy ra 2n+1=4k^2+4k+1, n=2k^2+2k, suy ra n chẵn
suy ra 3n+1 lẻ, từ 2 suy ra b lẻ. Đặt b=2p+1
(1)+(2) ta có 5n+2=4k^2+4k+1+4p^2+4p+1, suy ra 5n=4k(k+1)+4p(p+1)
suy ra 5n chia hết cho 8, suy ra n chia hết cho 8
Ta cần chứng minh n chia hết cho 5
Số chính phương có các tận cùng là 0,1,4,5,6,9
Lần lượt xét các trường hợp n=5q+1, 5q+2, 5q+3,5q+4, đều không thỏa mãn 2n+1, 3n+1 là số chính phương. Vậy n phải chia hêts cho 5
Mà 5 và 8 nguyên tố cùng nhau, nên n chia hết cho 40 (đpcm)

1.
\(2n+1\) luôn lẻ \(\Rightarrow2n+1=\left(2a+1\right)^2=4a^2+4a+1\Rightarrow n=2a\left(a+1\right)\)
\(\Rightarrow n\) chẵn \(\Rightarrow n+1\) lẻ \(\Rightarrow\) là số chính phương lẻ
\(\Rightarrow n+1=\left(2b+1\right)^2=4b^2+4b+1\)
\(\Rightarrow n=4b\left(b+1\right)\)
Mà \(b\left(b+1\right)\) là tích 2 số tự nhiên liên tiếp \(\Rightarrow\) luôn chẵn
\(\Rightarrow4b\left(b+1\right)⋮8\Rightarrow n⋮8\)
Mặt khác số chính phương chia 3 chỉ có các số dư 0 và 1
Mà \(\left(n+1\right)+\left(2n+1\right)=3n+2\) chia 3 dư 2
\(\Rightarrow n+1\) và \(2n+1\) đều chia 3 dư 1
\(\Rightarrow n⋮3\)
\(\Rightarrow n⋮24\) do 3 và 8 nguyên tố cùng nhau

Bạn tham khảo nhé ^^ http://olm.vn/hoi-dap/question/626962.html

\(\left(3^{n+1}-2.2^n\right)\left(3.3^n+2^{n+1}\right).3^{2n+2}+\left(8.2^{n-2}.3^{n+1}\right)^2\)
\(=\left(3^{n+1}-2^{n+1}\right)\left(3^{n+1}+2^{n+1}\right).3^{2n+2}+\left(2^{n+1}.3^{n+1}\right)^2\)
\(=\left(3^{2n+2}-2^{2n+2}\right).3^{2n+2}+2^{2n+2}.3^{2n+2}\)
\(=3^{2\left(2n+2\right)}-2^{2n+2}.3^{2n+2}+2^{2n+2}.3^{2n+2}\)
\(=3^{2\left(2n+2\right)}=\left(3^{2n+2}\right)^2\).
Ta thấy \(\left(3^{2n+2}\right)^2\)luôn là 1 số chính phương với mọi n\(\in\)N
Nên ta có ĐPCM.
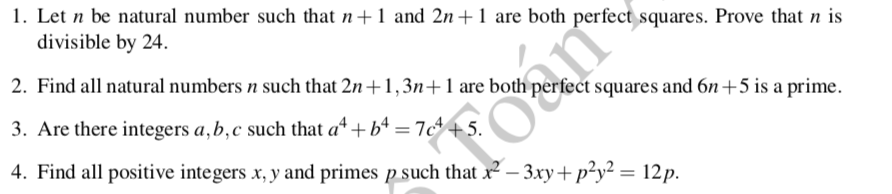
Vì 2n+1 là số CP lẻ => 2n+1 : 8 dư 1 => 2n chia hết cho 8
=> n chia hết cho 4 => n chẵn => n+1 lẻ => n+1 : 8 dư1
=> n chia hết cho 8 (*)
ta có n+1+2n+1=3n+2 _(đồng dư) _ 2 (mod 3)
màn+1 và 2n+1 _(đồng dư)_ 0(hoặc)1 (mod 3)
từ đó => n+1 và 2n+1 _(đồng dư)_ 1(mod 3)
=>n chia hết cho 3 (**)
từ (*) và (**) mà (3,8)=1 => n chia hết cho 24
=> đpcm