Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
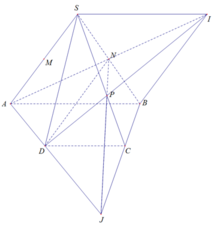
Xét (ABCD) có: A D ∩ B C = J
J ∈ BC ⇒ J ∈ (SBC)
Xét (SBC), Kẻ JN cắt SC tại P
Xét (SAB) và (SCD) có :
S là điểm chung
AB // CD
⇒ Giao tuyến là đường thẳng song song với AB
Mà I = A N ∩ D P
AN ⊂ (SAB)
DP ⊂ (SCD)
⇒ I nằm trên giao tuyến của 2 mặt phẳng
⇒ SI // AB
⇒ ASIB là hình thang có: SN = NB ( N là trung điểm SB)
⇒ ASIB là hình bình hành
M,N lần lượt là trung điểm của SB và SB là sai đề rồi bạn. Bạn coi lại đề nha
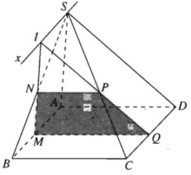
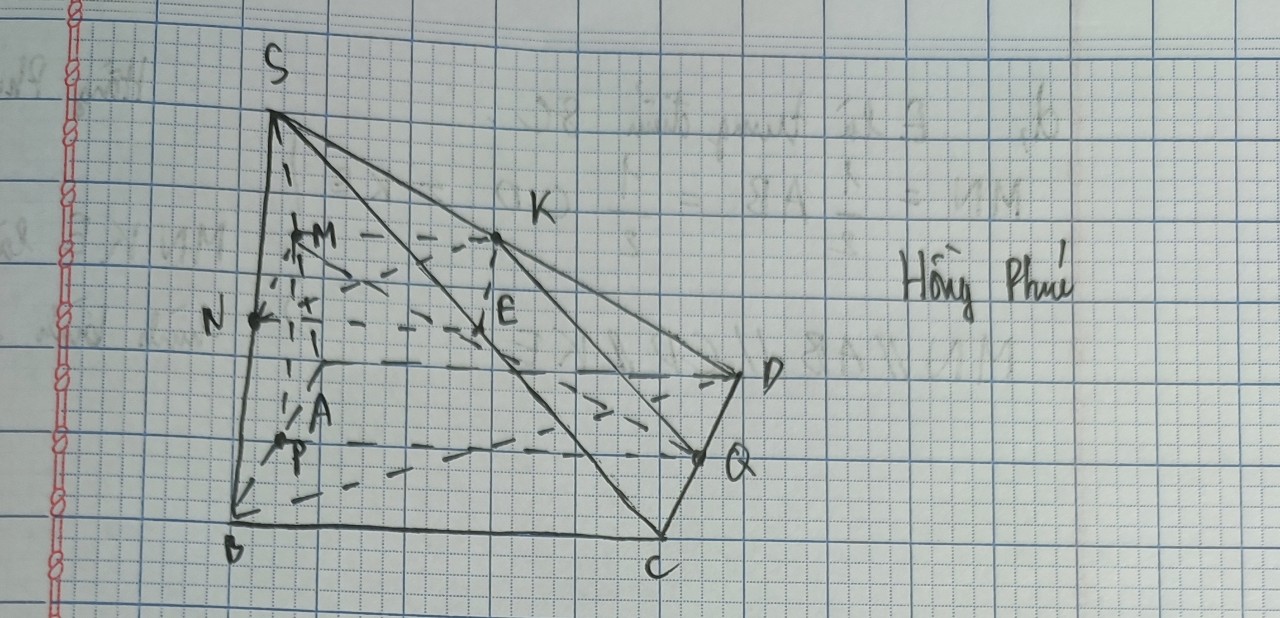
a) Vì M ∈ (SAB)
Và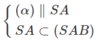 
nên (α) ∩ (SAB) = MN
và MN // SA
Vì N ∈ (SBC)
Và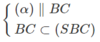 
nên (α) ∩ (SBC) = NP
và NP // BC (1)
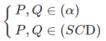⇒ (α) ∩ (SCD) = PQ
Q ∈ CD ⇒ Q ∈ (ABCD)
Và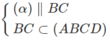 
nên (α) ∩ (ABCD) = QM
và QM // BC (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.
b) Ta có:
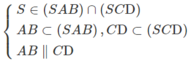⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
MN ∩ PQ = I ⇒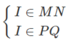 
MN ⊂ (SAB) ⇒ I ∈ (SAB), PQ ⊂ (SCD) ⇒ I ∈ (SCD)
⇒ I ∈ (SAB) ∩ (SCD) ⇒ I ∈ Sx
(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.
a: Ta có: CD//AB
AB\(\subset\)(SAB)
CD không nằm trong mp(SAB)
Do đó: CD//(SAB)
b: Xét ΔSBD có
M,N lần lượt là trung điểm của SB,SD
=>MN là đường trung bình của ΔSBD
=>MN//BD
Xét (CMN) và (ABCD) có
\(C\in\left(CMN\right)\cap\left(ABCD\right)\)
MN//BD
Do đó: (CMN) giao (ABCD)=xy, xy đi qua C và xy//MN//BD
a: Gọi O là giao điểm của AC và BD
Chọn mp(SAC) có chứa AN
\(O\in AC\subset\left(SAC\right);O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi I là giao điểm của SO với AN
=>I là giao điểm của AN với mp(SBD)
Chọn mp(AMN) có chứa MN
\(B\in AM\subset\left(AMN\right)\)
\(B\in BD\subset\left(SBD\right)\)
Do đó: \(B\in\left(AMN\right)\cap\left(SBD\right)\)
mà \(I\in\left(AMN\right)\cap\left(SBD\right)\)
nên (AMN) giao (SBD)=BI
Gọi K là giao điểm của BI với MN
=>K là giao điểm của MN với mp(SBD)
b: K là giao điểm của BI với MN
=>B,I,K thẳng hàng
d: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm của AC và O là trung điểm của BD
Xét ΔSAC có
O,N lần lượt là trung điểm của CA,CS
=>ON là đường trung bình
=>ON//SA và ON=SA/2
Xét ΔINO và ΔIAS có
\(\widehat{INO}=\widehat{IAS}\)
\(\widehat{NIO}=\widehat{AIS}\)
Do đó: ΔINO đồng dạng với ΔIAS
=>\(\dfrac{IN}{IA}=\dfrac{NO}{AS}=\dfrac{1}{2}\)
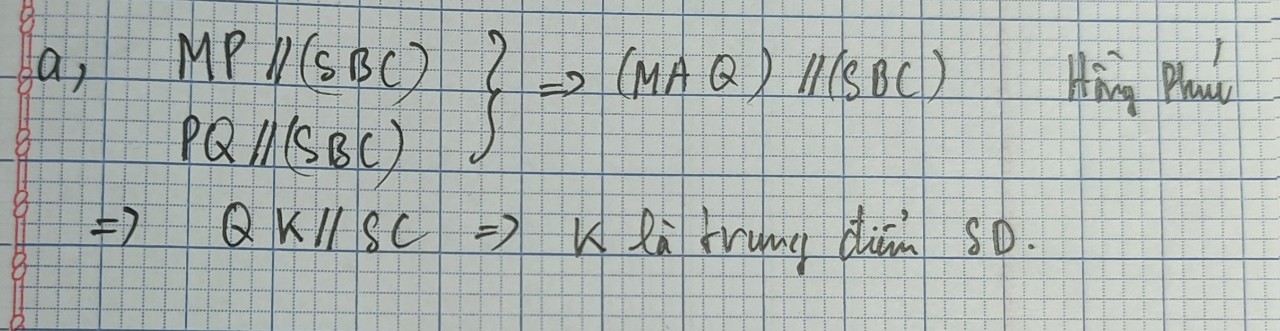
a: Xét ΔSAB có M,N lần lượt là trung điểm của SA,SB
=>MN là đường trung bình của ΔSAB
=>MN//AB
mà AB//CD
nên MN//CD
b: Trong mp(ABCD), gọi O là giao điểm của AC và BD
Trong mp(SBD), gọi K là giao điểm của DN và SO
Chọn mp(SAC) có chứa SC
\(K=DN\cap SO\)
=>\(K\in\left(DAN\right)\cap\left(SAC\right)\)
=>\(\left(DAN\right)\cap\left(SAC\right)=AK\)
Gọi P là giao điểm của AK với SC
=>P là giao điểm của SC với (DAN)