Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta thấy bán kính đường tròn ngoại tiếp thì bằng 1313 đường cao.
Mà đường cao thì bằng √3232 cạnh.
Nên cạnh của tam giác gấp 2√323 bán kính, tức là bằng 2√3r23�.
Diện tích 2√3r.3r2=3√3r223�.3�2=33�2.
Để chứng minh diện tích của tam giác đều ngoại tiếp đường tròn bán kính r bằng 3r^2, ta sẽ sử dụng các công thức và tính chất của tam giác đều và đường tròn.
Giả sử tam giác đều ngoại tiếp đường tròn có tâm O và bán kính r. Đường tròn này cắt tam giác đều tại các đỉnh A, B và C.
Để tính diện tích của tam giác đều ABC, ta sẽ sử dụng công thức diện tích tam giác đều:
Diện tích tam giác đều ABC = (cạnh)^2 * sqrt(3) / 4
Với tam giác đều ngoại tiếp đường tròn, cạnh tam giác bằng đường kính của đường tròn, tức là 2r.
Diện tích tam giác đều ABC = (2r)^2 * sqrt(3) / 4
= 4r^2 * sqrt(3) / 4
= r^2 * sqrt(3)
Vậy diện tích của tam giác đều ngoại tiếp đường tròn bán kính r là r^2 * sqrt(3).
Để chứng minh r^2 * sqrt(3) = 3r^2, ta sẽ sử dụng tính chất của căn bậc hai:
sqrt(3) = sqrt(3) * sqrt(1) = sqrt(3 * 1) = sqrt(3) * sqrt(3) / sqrt(3) = 3 / sqrt(3)
Vậy r^2 * sqrt(3) = r^2 * (3 / sqrt(3)) = 3r^2.
Vậy ta đã chứng minh được diện tích của tam giác đều ngoại tiếp đường tròn bán kính r bằng 3r^2.


Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC.
Ta có: BC = 2R
Giả sử đường tròn (O) tiếp với AB tại D, AC tại E và BC tại F
Theo kết quả câu a) bài 58, ta có ADOE là hình vuông.
Suy ra: AD = AE = EO = OD = r
Theo tính chất hai tiếp tuyến cắt nhau ta có:
AD = AE
BD = BF
CE = CF
Ta có: 2R + 2r = BF + FC + AD + AE
= (BD + AD) + (AE + CE)
= AB + AC
Vậy AB = AC = 2(R + r)

Tìm ba phân số khác nhau biết phân số thứ nhất và phân số thứ hai là 7/8,tổng của phân số thứ hai và phân số thứ ba là 8/7,tổng của phân số thứ nhất và phân số thứ ba là 8/9

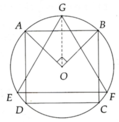
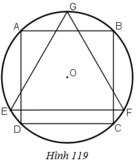
a, V h t A B C D = π AB 2 2 . BC = π AB 3 4 = π 2 2 . R 3 (1)
V h c = 4 3 πR 3 (2)
V h n = 1 3 π EF 2 2 . GH = 1 8 3 π . EF 3 . Tính được GO = 3 R
=> V h n = 1 8 3 π 3 3 R 3 = 3 8 πR 3 (3)
Từ (1), (2) và (3) => ĐPCM
b, S t p h t = 3 πR 2 (4); S h c = 4 πR 2 (5)
S t p h n = 3 4 πEF 2 = 3 4 π . 3 R 2 = 9 4 πR 2 (6)
Từ (4); (5) và (6) => ĐPCM
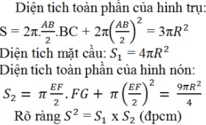
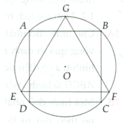
Ta thấy bán kính đường tròn ngoại tiếp thì bằng \(\dfrac{1}{3}\) đường cao.
Mà đường cao thì bằng \(\dfrac{\sqrt{3}}{2}\) cạnh.
Nên cạnh của tam giác gấp \(2\sqrt{3}\) bán kính, tức là bằng \(2\sqrt{3}r\).
Diện tích \(\dfrac{2\sqrt{3}r.3r}{2}=3\sqrt{3}r^2\).