Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có : \(\frac{\sqrt{2}+1}{\sqrt{2}-1}=\frac{\left(\sqrt{2}+1\right)\left(\sqrt{2}+1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}=\frac{\left(\sqrt{2}+1\right)^2}{2-1}=\left(\sqrt{2}+1\right)^2\)
\(=2+2\sqrt{2}+1=3+2\sqrt{2}\)
b, Ta có : \(\sqrt{\frac{4}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\frac{4}{\left(2+\sqrt{5}\right)^2}}=\frac{2}{\sqrt{5}-2}-\frac{2}{2+\sqrt{5}}\)
\(=\frac{2\left(\sqrt{5}+2\right)}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}-\frac{2\left(2-\sqrt{5}\right)}{\left(2+\sqrt{5}\right)\left(2-\sqrt{5}\right)}=2\sqrt{5}+4+4-2\sqrt{5}=8\)
bài đó câu 1 sai đề câu 2 chỉ cần nhân cả 2 vế với căn 2 rồi áp dụng hđt 1,2 vào là được nha

a) \(A=\frac{2+\sqrt{3}}{\sqrt{2}+\sqrt{2+\sqrt{3}}}+\frac{2-\sqrt{3}}{\sqrt{2}-\sqrt{2-\sqrt{3}}}=\sqrt{2}\)
Biến đổi vế trái :
VT = \(\frac{2+\sqrt{3}}{\sqrt{2}+\sqrt{2+\sqrt{3}}}+\frac{2-\sqrt{3}}{\sqrt{2}-\sqrt{2-\sqrt{3}}}\)
\(=\frac{\sqrt{2}\left(2+\sqrt{3}\right)}{\sqrt{2}\left(\sqrt{2}+\sqrt{2+\sqrt{3}}\right)}+\frac{\sqrt{2}\left(2-\sqrt{3}\right)}{\sqrt{2}\left(\sqrt{2}-\sqrt{2-\sqrt{3}}\right)}\)
\(=\frac{\sqrt{2}\left(2+\sqrt{3}\right)}{2+\sqrt{4+2\sqrt{3}}}+\frac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\sqrt{4-2\sqrt{3}}}=\frac{\sqrt{2}\left(2+\sqrt{3}\right)}{2+\left|\sqrt{3}+1\right|}+\frac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\left|\sqrt{3}-1\right|}\)
\(=\frac{\sqrt{2}\left(2+\sqrt{3}\right)}{2+\sqrt{3}+1}+\frac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\sqrt{3}+1}=\frac{\sqrt{2}\left(2+\sqrt{3}\right)}{\sqrt{3}+3}+\frac{\sqrt{2}\left(2-\sqrt{3}\right)}{3-\sqrt{3}}=\frac{\sqrt{2}\left(2+\sqrt{3}\right)\left(\sqrt{3}-3\right)+\sqrt{2}\left(2-\sqrt{3}\right)\left(\sqrt{3}+3\right)}{\left(\sqrt{3}+3\right)\left(3-\sqrt{3}\right)}\)
\(=\frac{\sqrt{2}\left(6-2\sqrt{3}+3\sqrt{3}-3+6+2\sqrt{3}-3\sqrt{3}-3\right)}{9-3}=\frac{6\sqrt{2}}{6}=\sqrt{2}=VP\left(đpcm\right)\)
b) \(B=\left(5+\sqrt{21}\right)\left(\sqrt{14}-\sqrt{6}\right)\sqrt{5-\sqrt{21}}=8\)
Biến đổi vế trái :
VT = \(\left(5+\sqrt{21}\right)\left(\sqrt{14}-\sqrt{6}\right)\sqrt{5-\sqrt{21}}=\sqrt{5+\sqrt{21}}\left(\sqrt{14}-\sqrt{6}\right)\sqrt{5+\sqrt{21}}\sqrt{5-\sqrt{21}}\)
\(=\sqrt{2}\sqrt{5+\sqrt{21}}\left(\sqrt{7}-\sqrt{3}\right)\sqrt{25-21}=\sqrt{10+2\sqrt{21}}\left(\sqrt{7}-\sqrt{3}\right)\sqrt{4}=\left|\sqrt{7}+\sqrt{3}\right|\left(\sqrt{7}-\sqrt{3}\right)2\)
\(=\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)2=\left(7-3\right)2=4.2=8=VP\left(đpcm\right)\)

\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7\)
\(=16-8\sqrt{7}+7=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot2+4}-\sqrt{5}\)
\(=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}\)
\(=\left|\sqrt{5}-2\right|-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}\)
\(=\dfrac{\sqrt{3-2\cdot\sqrt{3}\cdot1+1}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}=\dfrac{3-1}{2-1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\dfrac{6\sqrt{6}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{1}{2}\sqrt{6}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{1}{2}-2=-\dfrac{3}{2}=-1,5\)
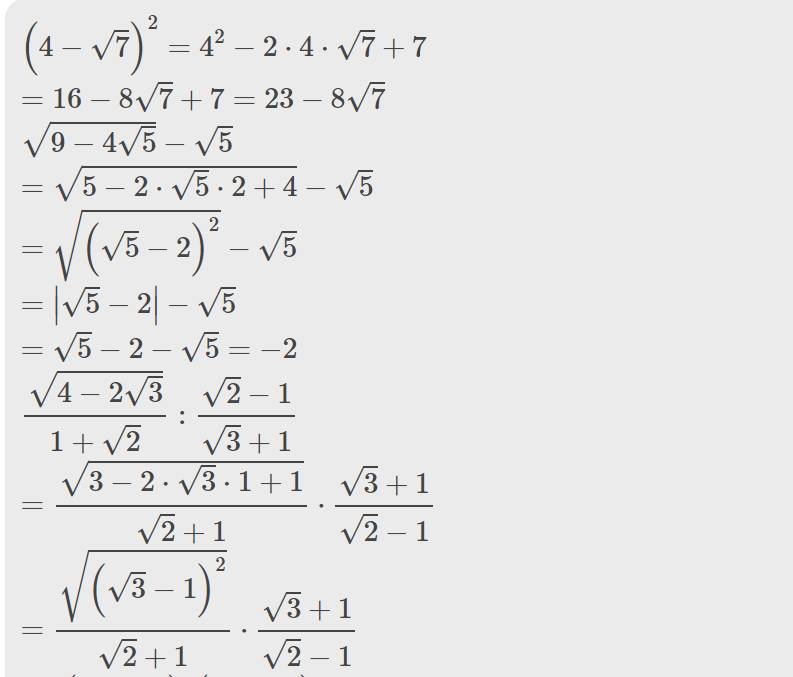
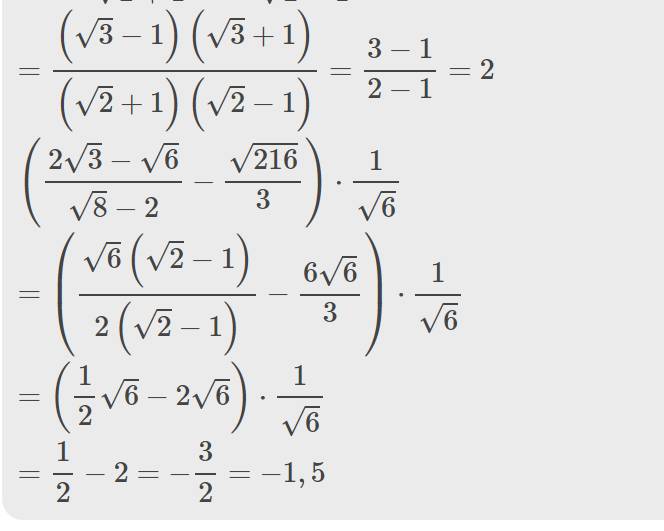
Ta có VT: \(\sqrt{\frac{4}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\frac{4}{\left(2+\sqrt{5}\right)^2}}\)=\(\frac{\sqrt{4}}{\sqrt{\left(2-\sqrt{5}\right)^2}}-\frac{\sqrt{4}}{\sqrt{\left(2+\sqrt{5}\right)^2}}\)
=\(\frac{2}{\left|2-\sqrt{5}\right|}-\frac{2}{\left|2+\sqrt{5}\right|}\)
=\(\frac{2}{\sqrt{5}-2}-\frac{2}{2+\sqrt{5}}\)
=\(\frac{2.\left(2+\sqrt{5}\right)-2.\left(\sqrt{5}-2\right)}{\left(\sqrt{5}-2\right).\left(2+\sqrt{5}\right)}\)
=\(2.\left(2+\sqrt{5}\right)-2.\left(\sqrt{5}-2\right)\)
=\(4+2\sqrt{5}-2\sqrt{5}+4\)
=8 (bằng VP)
mình bt làm nhưng ko bt bấm phân số