
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


VT = \(\frac{1-cosx+cos2x}{sin2x-sin}\)
= \(\frac{1-cosx+2cos^2x-1}{2sinx.cosx-sinx}\)
= \(\frac{cosx\left(2cosx-1\right)}{sinx\left(2cosx-1\right)}\)
= cotx = VP ( đpcm )


\(=1-\dfrac{sin^2x}{1+\dfrac{cosx}{sinx}}-\dfrac{cos^2x}{1+\dfrac{sinx}{cosx}}=1-\dfrac{sin^3x}{sinx+cosx}-\dfrac{cos^3x}{sinx+cosx}\)
\(=1-\dfrac{sin^3x+cos^3x}{sinx+cosx}=1-\dfrac{\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)}{sinx+cosx}\)
\(=1-\left(1-sinx.cosx\right)=sinx.cosx\)

\(\sin^4x-\cos^4x=\left(\sin^2x+\cos^2x\right)\left(\sin^2x-\cos^2x\right)=\sin^2x-\cos^2x\)

\(\frac{sin4x-sin2x}{1-cos2x+cos4x}=\frac{2sin2x.cos2x-sin2x}{1-cos2x+2cos^22x-1}=\frac{sin2x\left(2cos2x-1\right)}{cos2x\left(2cos2x-1\right)}=\frac{sin2x}{cos2x}=tan2x\)
\(\Rightarrow\) đề sai
b/
\(\frac{1-cos4x}{sin4x}=\frac{1-\left(1-2sin^22x\right)}{2sin2x.cos2x}=\frac{2sin^22x}{2sin2x.cos2x}=\frac{sin2x}{cos2x}=tan2x\)
Đề sai tiếp lần 2

\(\frac{sinx+sin5x+sin3x}{cosx+cos5x+cos3x}=\frac{2sin3x.cos2x+sin3x}{2cos3x.cos2x+cos3x}=\frac{sin3x\left(2cos2x+1\right)}{cos3x\left(2cos2x+1\right)}=\frac{sin3x}{cos3x}=tan3x\)

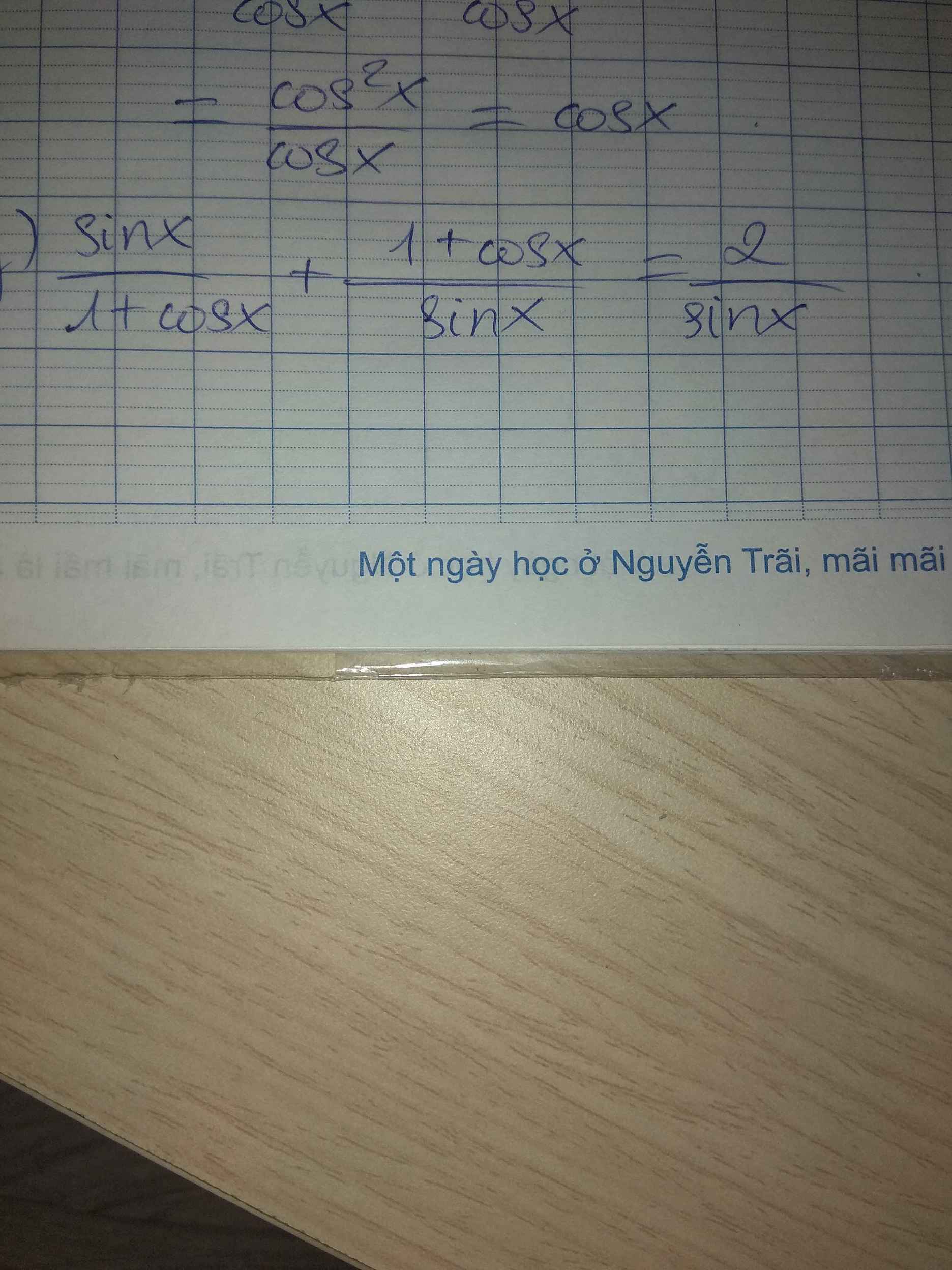
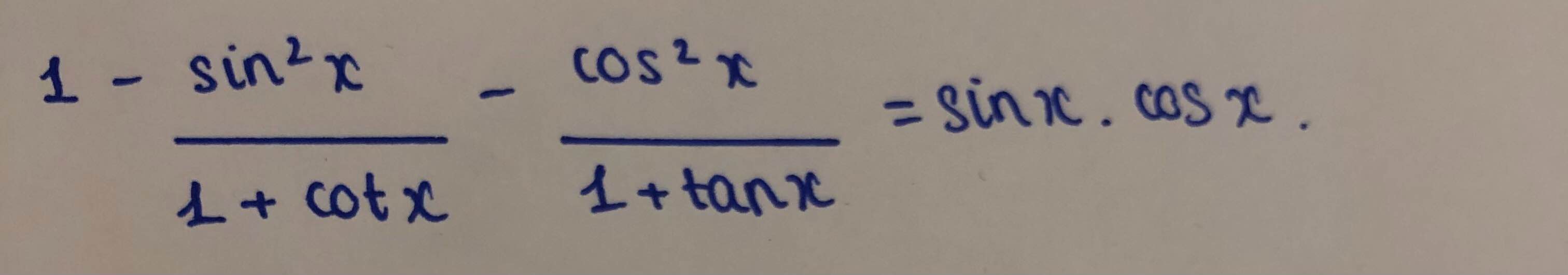
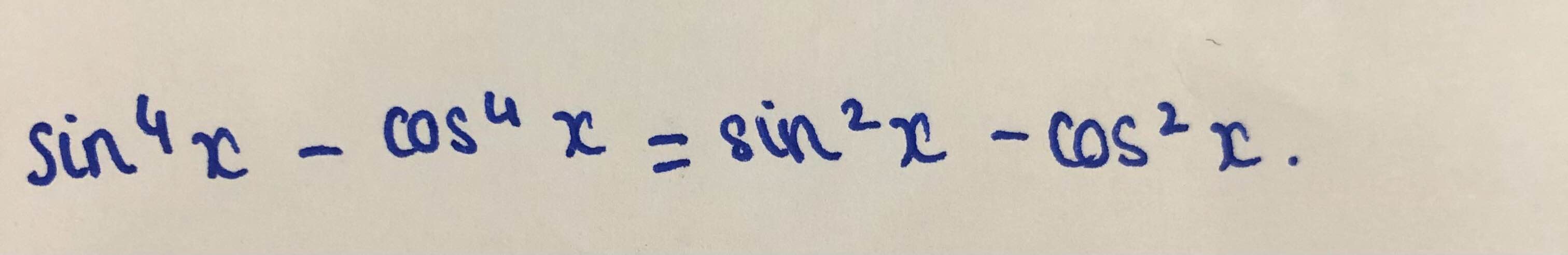
\(\frac{\left(sin^2x\right)^2-\left(cos^2x\right)^2}{2sinxcosx}\)=\(\frac{\left(sin^2x+cos^2x\right).\left(sin^2x-cos^2x\right)}{2sinxcosx}\)=\(\frac{1.\left(sin^2x-cos^2x\right)}{2sinxcosx}\)=\(\frac{sin^2x-cos^2x}{sin2x}\)=\(\frac{\frac{1-cos2x}{2}-\frac{1+cos2x}{2}}{sin2x}\)=\(\frac{1-1-cos2x-cos2x}{2}.\frac{1}{sin2x}\)=\(\frac{-2cos2x}{2sin2x}=\frac{-cos2x}{sin2x}=-cot2x\left(đpcm\right)\)